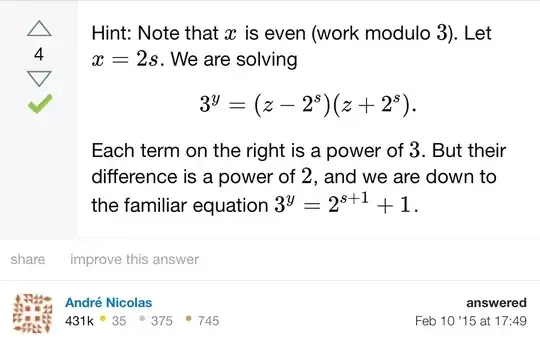
Question: Determine all pairs of positive integers $(x,y)$ for which $2^x+3^y$ is a perfect square.
Doubt: This question was posted before and a screenshot of one of the hints is attached. I don't understand how do we arrive at $ 2^{s+1} +1=3^y$.
Doesn't that require us to assume the factors are $1$ and $3^y$? Why can't both the factors be powers of three other than $0$?