Ideal angle to launch from a swing to maximize distance

Question

When I was little (and even now if I can get the chance) I liked to play on swings, and my favorite method of dismounting was to let go mid-swing and fly thru the air.

That got me wondering what the best point is to let go of a swing to maximize the landing distance. Naively, one might think the point is where the swing makes a $45^\circ$ angle with the vertical, but that may not be so, because with a swing (unlike a cannon), the launch speed decreases with launch angle. Further complicating matters, the landing distance is short enough to be comparable to the length of the swing, meaning that the mere extra initial distance you get from launching late in a swing (some fraction of the swing's length) could be a significant addition to the distance traveled upon landing.

So the question is: At what point in a swing should a person let go to maximize the landing distance?

Note: I give my own answer to this question below, but it's only one method of tackling the problem. Other answers making use of different assumptions, approximations, techniques, etc. are most certainly welcome! That's part of the reason I left the question statement rather general.

Answer 1

Here is the general solution in the released pendulum model (since you asked me to post it).

Here is the definition of my variables:

• $h$ is the height of the swing off the ground when it's at rest
• $m$ is the maximum additional height above $h$ it swings to
• $\ell$ is the length of the swing rope
• $x,y$ are the position of the swing at release in coordinates where the height $h$ off the ground is taken as $0$ height and $x$ is measured from the swing at rest
• $v_x,v_y$ are the $x,y$ components of the velocity at $x,y$
• $\theta$ is the swing angle you release at (measured from $0$ at rest)
• $\theta_m$ is the maximum angle you would swing to if you didn't release
• $x_\text{land}$ is the distance you travelled

Energy conservation gives $\frac{1}{2}v^2+gy=gm$ which gives our total velocity $v$: $$v^2=2g(m-y)$$

Our coordinate system gives us: \begin{align*} x&=\ell\sin\theta \\ y&=\ell-\ell\cos\theta \\ v_x&=v\cos\theta \\ v_y&=v\sin\theta \end{align*}

Considering $y$ kinematics when you land (at vertical coordinate $=-h$) gives you flight time. $$-h=y+v_yt-gt^2/2\implies t=\frac{v_y}{g}\left(1+\sqrt{1+\frac{2g(y+h)}{v_y^2}}\right)$$

The $x$ kinematics give you the distance you travel. \begin{align*} x_\text{land}&=x+v_xt\text{ (and now just plug in and we are done)} \\ &=x+\frac{v_xv_y}{g}\left(1+\sqrt{1+\frac{2g(y+h)}{v_y^2}}\right) \\ &=x+\frac{v^2\sin(2\theta)}{2g}\left(1+\sqrt{1+\frac{2g(y+h)}{v_y^2}}\right) \\ &=x+\sin(2\theta)(m-y)\left(1+\sqrt{1+\frac{2g(y+h)}{v^2\sin^2\theta}}\right) \\ &=x+\sin(2\theta)(m-y)\left(1+\sqrt{1+\frac{y+h}{(m-y)\sin^2\theta}}\right) \\ &=\ell\sin\theta+\sin(2\theta)(m-\ell+\ell\cos\theta)\left(1+\sqrt{1+\frac{\ell-\ell\cos\theta+h}{(m-\ell+\ell\cos\theta)\sin^2\theta}}\right) \end{align*}

The $\theta$ you're interested in is the unique maximum of $x_\text{land}$ satisfying $0\leq\theta\leq\theta_m$. Since $\theta_m$ is the max swing angle, we can relate it to max height $m$ by $m=\ell-\ell\cos\theta_m$. From this you can see the parameter $m$ is just given by the max angle, so you can replace it.

$$x_\text{land}=\ell\sin\theta+\ell\sin(2\theta)(\cos\theta-\cos\theta_m)\left(1+\sqrt{1+\frac{\ell-\ell\cos\theta+h}{\ell(\cos\theta-\cos\theta_m)\sin^2\theta}}\right)$$

You can make this 'unitless' by switching to units where $\ell=1$ (which is how I work on my paper). To go back to units, everywhere you see a variable with units of distance replace it with the same variable divided by $\ell$ to get the unitful equation again.

$$x_\text{land}=\sin\theta+\sin(2\theta)(\cos\theta-\cos\theta_m)\left(1+\sqrt{1+\frac{1-\cos\theta+h}{(\cos\theta-\cos\theta_m)\sin^2\theta}}\right)$$

To use this to find the release angle you pick $h\geq 0$ and $0<\theta_m\leq\pi/2$ then numerically solve $\frac{\mathrm{d}x_\text{land}}{\mathrm{d}\theta}=0$ for $\theta$ subject to the constraint $0\leq\theta\leq\theta_m$.

Here are some plots over all $\theta_m$. I'm plotting the fraction of maximum swing angle you release at, $\theta/\theta_m$.

$h=0$:

$h=\ell/2$:

$h=\ell$:

The system you used is the one when $h=0$ and $\theta_m=\pi/2$.

Answer 2

$\require{begingroup}\begingroup$ Here is the setup:

That is, $H$ is the height of the swing set, $\theta$ is the angle the swing deviates from rest, $v_0$ is the launch speed, $x_0$ and $y_0$ are the position coordinates of launch, and $x$ is the final landing position.

For this problem, I assume that before launch, you are swinging the full $-90^\circ$ to $90^\circ$ thereby maximizing the would-be launch speed at each $\theta$. I also assume that the swing's length is the same as its height (i.e. at rest, the swing's seat just barely touches the ground). This simplification seems justified since (on a real swing) when you land, your bottom will likely be at about the same height that the swing's seat would be at rest (well, assuming you land on your feet $\overset{.\ .}{\smile}$).

Now, with a little geometry, you can convince yourself that the angle of launch is the same as the angle of swing. Knowing this, the problem of figuring out where you land given a launch angle reduces to a projectile motion problem if we can figure out how $v_0$ varies against $\theta$.

To do so, let's analyze the energy conservation equation for this setup: $\newcommand{\KE}{\operatorname{KE}} \newcommand{\PE}{\operatorname{PE}}$ \begin{align} \KE_0 + \PE_0 &= \PE_\mathrm{max} \\ \frac{1}{2} mv_0^2 + mgy_0 &= mgH \\ \implies v_0^2 &= 2g(H-y_0) \end{align} Now, looking at the picture, we see that $$ \cos\theta = \frac{H-y_0}{H} \iff H-y_0 = H \cos \theta $$ So we get for $v_0^2$: $$ v_0^2 = 2gH \cos \theta $$ So now we know how $v_0$ varies against $\theta$. To compute how far you (our projectile) fly, we need to know how long you will be in the air. We can do this using the projectile equation $$ \Delta y = v_0 t + \frac{1}{2} at^2 $$ In our case: \begin{align} &-y_0 = (v_0 \sin\theta)t - \frac{1}{2} gt^2 \\ \iff &\frac{1}{2} gt^2 - (v_0 \sin\theta)t - y_0 = 0 \end{align} Using the quadratic formula, we obtain $$ t = \frac{v_0 \sin\theta + \sqrt{v_0^2 \sin^2\theta+2gy_0}}{g} $$ and after plugging in the appropriate expressions for $v_0$ and $y_0$ and simplifying we get $$ t = \sqrt{\frac{2H}{g}} \cdot \left(\sin\theta \sqrt{\cos\theta} + \sqrt{1-\cos^3\theta} \right) $$ Now that we have the travel time, we can compute the horizontal distance using this formula: $$ x = (v_0 \cos\theta)t + x_0 $$ where the geometry of the picture tells us $x_0 = H \sin\theta$.

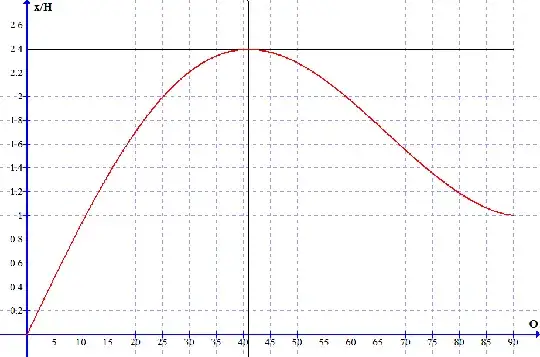
Plugging in the various expressions and simplifying, we get $$ x = H \cos\theta \cdot \left(\sin 2\theta + 2\sqrt{\cos\theta - \cos^4\theta} \right) + H \sin\theta $$ whose derivative we can take to find the maximum. Using Wolfram|Alpha, I got an optimal launch angle of approximately $0.7153$ radians or about $41^\circ$.

Wolfram|Alpha also provided an exact closed form for the solution. It was very ugly, but did lend itself to some simplification. So for those (like me) who enjoy seeing solutions in their full, unabashed glory, here it is: $$ \theta = 2 \arctan\sqrt{\frac{\sqrt[3]{4\beta} - 10\sqrt[3]{2/\beta}-1}{3}} $$ where $$ \beta = 11+3\sqrt{69} $$ If we now take this result and plug it into our original expression for $x$, we can compute what the actual maximum distance is. It is given approximately by $$ \max(x) \approx 2.39354 \, H $$ where $H$, recall, is the height/length of the swing.

(And yes, Wolfram did provide an exact closed form for the $2.39354$ factor, but it is way too long to write down here. Nevertheless, if you're still interested, you can view it here.)

A graph of landing distance per unit swing height ($x/H$) vs launch angle ($\theta$) seems to confirm our results:

Finally, we can also compute the maximum height you will attain after launching from the ideal angle. There are many ways to compute this. I choose to do so using the energy conservation equations again. The maximum height will occur when you are traveling horizontally only and not moving either higher or lower: that is, when your speed is $v_0 \cos\theta$. \begin{align} \PE_\mathrm{max} &= \PE_1 + \KE_1 \\ \iff mgH &= mgy_\mathrm{max} + \frac{1}{2} m(v_0 \cos\theta)^2 \\ \implies y_\mathrm{max} &= H - \frac{1}{2g} v_0^2 \cos^2\theta \\ &= H - \frac{1}{2g} (2gH \cos\theta) \cos^2\theta \\ &= H - H \cos^3\theta \\ &= H(1 - \cos^3\theta) \end{align} Plugging in the ideal angle, we get $$ y_\mathrm{max} \approx 0.5698 H $$ (don't ask about the closed form...)

which tells us that, unless you're okay with falling about half the height of your swing set, don't try this at home...

---

Some follow up questions I didn't try to answer:

• How does the answer change if the swing seat is not assumed to be touching the ground at rest? (e.g. a rope swing, where your lowest point in swing is significantly above the water surface)
• What do the ideal angles look like if we don't start with maximum momentum, i.e. a $-90^\circ$ to $90^\circ$ initial swing?

$\endgroup$