12

The minimal number of squares for rectangles up to longest side 380 is known. The data was calculated for the question "tiling a rectangle with the smallest number of squares". I took a look at hard cases for aspect ratios under 2.

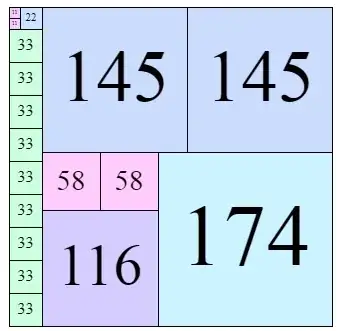
323,319

323,293

f(323,319)=18. (shown above)
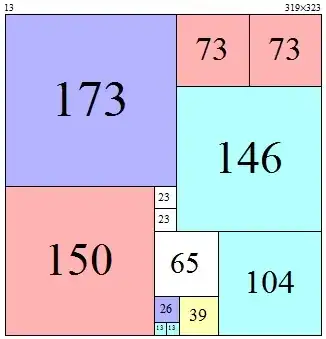
f(323,293)=17. (shown above, along with f(30,293)=17)
f(323,317)=16.
f(323,283)=16.
f(323,281)=16.

Those are all of the cases up to 380 that need more than 15 squares. For 15 squares, add the value 352 as hard.

f(323,X)=15, with X in {256, 271, 277, 307, 313}
f(352,X)=15, with X in {283, 289, 293, 299, 307, 311, 317, 325, 329, 331, 333, 343, 347, 349, 351}

For rectangles needing 14 squares, more than half the values have larger side 323 or 352.

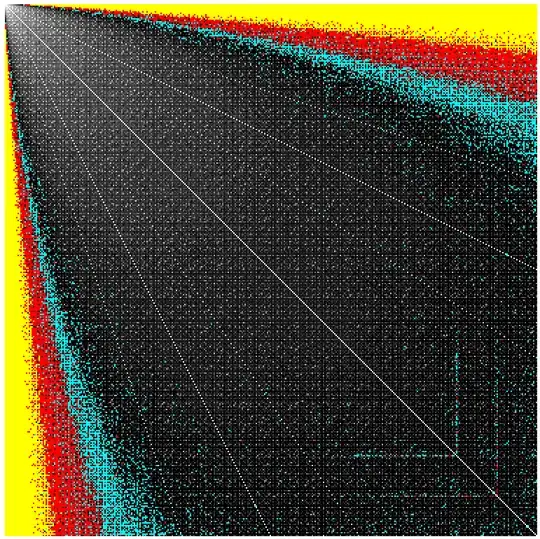
If f(a,b) is the minimal number of squares needed for an aXb rectangle, an array plot of those values looks like the following, with gray levels for 1 to 13 squares, cyan for 14 squares, red for 15-18 squares, and yellow for 19+ squares. The anomalies are at 323 and 352.

squares needed

What is special about 323 (and 352) and squared rectangles?

For rectangles with aspect ratios under 2 and relatively prime sides, calculate the average number of squares needed for a given longest edge. By the oblong conjecture, subtract (edge)^(1/3) +6. The last two spikes are at 323 and 352. The middle spike is at 180.

hard edges

Where is the next hard value after 180, 323, 352?

UPDATE: As shown in the answer below, some better solutions exist for f(323,319). So it turns out there is nothing special about 323, it's just a runtime glitch of some sort on those two rows. Indeed, it turns out a 13 square solution exists for 323x319.

323x319

Ed Pegg
  • 21,868

1 Answers1

4

The three rectangles displayed are each composed of 3 sub-rectangles, and each of those sub-rectangles has it's tiling determined by the continued fraction from the Euclidean GCD algorithm. You could just use the Euclidean GCD to get a squaring of the 323x319 rectangle, but it wouldnt be minimal. The continued fraction of 323/319 = [1; 79,1,3], ie 323x319 = 1x319^2 + 79x4^2 + 1x3^2 + 3x1^2, and the sum of the c.f. values gives the order of the squared rectangle, ie 1+79+1+3 = 84, which is certainly not minimal.

However if the rectangle is dissected into several rectangles the order can be reduced.

For the three examples;

323x319 = 290x145 + 290x174 + 319x33

cont.frac [2] [1;1,2] [9,1,2] sum = 18

323x30 = 260x30 + 30x18 + 30x15

cont.frac [8;1,2] [1;1,2] [2] sum = 17

323x293 = 255x153 + 255x170 + 323x38 = 17

cont.frac [1;1,2] [1,2] [8,2] sum = 17

All the examples have three subrectangles and are minimal, so for these no better solutions exist with rectangles composed of just two subrectangles.

It would be worth checking to see if perhaps 323 and 352 are the first time a minimal solution requires 3 subrectangles. If all other smaller rectangles had only required dissection into 1 or 2 subrectangles, and if the average number of squares in a small rectangle was only half a dozen or so, then 3 rectangle solutions would jump from orders of 6 - 12 to 18 or thereabouts, and the next jump might occur when the first 4 subrectangle solutions appear.

Stuart Anderson
  • 109