Dog and Goose Circular Pursuit Problem

Question

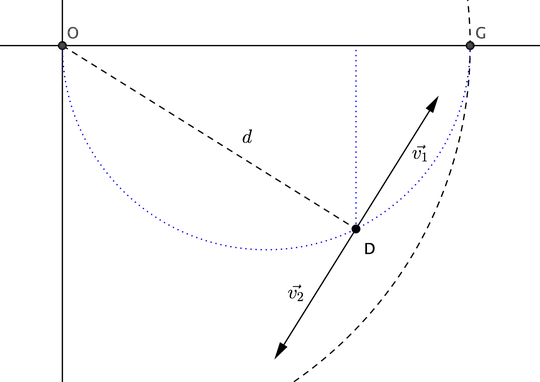
Imagine there is a Goose swimming counter-clockwise at the edge of a circular pond of radius $R$, and a dog (starting at the center of the pond) is paddling to catch it such that the dog is always pointing towards the goose. If the goose is travelling at speed $u$, what is the minimum speed that the dog must travel in order to eventually catch the goose? What is the minimum speed needed for the dog to catch the goose in time $\tau$?

I've seen pursuit problems like this in my Dynamical Systems textbook (indeed, this is very similar to one) and I've never had any luck solving them. I've found some solutions online to certain problems, but they tend to explain it very poorly in my opinion (for the record, all solutions I've seen to circular pursuit problems involve introducing alternate coordinate systems)

My attempt:

Let $x_d$ be the position vector of the dog, $x_g$ be the position vector of the goose, and $v_d$ be the velocity vector of the dog.

Drawing a diagram makes it evident that for any speed $||v_d||$ at fixed time $t$, $\exists \lambda \in \mathbb{R}$ s.t.

$$x_d + \lambda v_d = x_g = (R \cos(u t/R), R \sin(ut/R))$$

Generally, $\lambda = \lambda(t)$, which makes this much more difficult, but we are able to get two differential equations out of it:

$$x_d' + \frac{x_d}{\lambda(t)} = \frac{R}{\lambda(t)} \cos(ut/R) $$

$$y_d' + \frac{y_d}{\lambda(t)} = \frac{R}{\lambda(t)} \sin(ut/R) $$

Which is a first-order linear ODE, but I don't even know if the integrating factor $exp(\int \frac1{\lambda(t)} dt)$ exists, let alone how to find $\lambda(t) $

In order to catch the goose, we'd need $||x_d - x_g|| = 0$ for some $t \in \mathbb {R} $.

I believe the minimum would occur when

$||x_d - x_g|| \ne 0 \space\space \forall t \in \mathbb {R} \space \text { with } \space \lim_{t \to \infty} ||x_d - x_g|| = 0$.

As mentioned, I'm not sure how I'd find $\lambda $ if it's even worthwhile to introduce to the problem (I originally debated trying Lagrange multipliers or two-timing for this part, but am unsure how if it's possible).

I am open to seeing alternative methods as well as seeing if there's any way to actually use my thought process.

I am also aware that pursuit problems often lack a closed solution, but I thought I'd try my hand it nonetheless.

Answer 1

We can get a simpler understanding of the problem if we look at dog's path in a frame which is rotating counterclockwise with angular velocity $\omega=u/R$ around the circle center. In such a frame the goose is sitting still at $G=(R,0)$, while the velocity of dog $D$ is made up of two contribution: $\vec{v_1}$, directed along $DG$ and of fixed magnitude $v$, and $\vec{v_2}$, due to the frame rotation, perpendicular to line $OD$ and of magnitude $\omega d$, where $d=OD$ is the distance of the dog from the center.

One can then write down at once a pair of coupled differential equation for the position $(x(t),y(t))$ of the dog. To keep them as simple as possible I conveniently set the unit of length so that $R=1$: $$ \begin{align} & x'(t)=\frac{(1-x)}{\sqrt{(1-x)^2+y^2}}v+\omega y,\\ &y'(t)=-\frac{y}{\sqrt{(1-x)^2+y^2}}v-\omega x\\ \end{align} $$ Notice that these are invariant under the scaling $(v,\omega,t)\to(kv,k\omega,t/k)$, so that the shape of dog's path depends only on the ratio $v/\omega$, as one could expect.

If the dog reaches a point where $\vec{v_1}=-\vec{v_2}$, then it stands there forever. That happens if $\omega d=v$, that is $d=v/\omega$, and if at the same time $OD\perp DG$, that is if $D$ belongs to the circle of diameter $OG$ (see picture below). A simple geometrical reasoning allows then to compute the coordinates of this halting point: $x=v^2/\omega^2$, $y=-(v/\omega)\sqrt{1-v^2/\omega^2}$.

I tried to get an exact solution of the above differential equations with Mathematica, but to no avail. But they can be solved numerically: I plotted the resulting dog's path for ten values of $v/\omega$, from $0.1$ to $1$ (picture below). In any case the path reaches asymptotically the corresponding halting point. For small values of $v/\omega$, this occurs after a long spiralling around it. For values near to $1$ there is no spiral.

As one could expect, for $v/\omega<1$ the dog doesn't catch the goose. For $v/\omega>1$ dog's path is very similar to the one shown above for $v/\omega=1$, and numerical solutions show that the dog arrives at $G$ in a finite time (which is quite obvious). For $v/\omega=1$ I expect the dog doesn't arrive there in a finite time, but that is hard to tell from a numerical solution.

In that case, we can try to compute directly the time taken by the dog to catch the goose, based on the evidence that the last part of dog's path, for $v/\omega=1$, is very near to the halting-points circle. If $s$ is the distance $DG$, we know from the above discussion that if $D$ is on that circle then dog's velocity is directed towards $G$ and its magnitude is given by $v-\omega d=v\big(1-\sqrt{1-s^2}\big)$. It follows that $$ {ds\over dt}=-v\big(1-\sqrt{1-s^2}\big), $$ and the time $t_0$ taken to travel a final length $s_0$ is then $$ t_0=\int_0^{t_0}dt=-{1\over v}\int_{s_0}^0{ds\over\big(1-\sqrt{1-s^2}\big)}. $$ But the last integral is divergent, so we can safely conclude that if $v/\omega=1$ the dog won't catch the goose.

EDIT.

The equations of motion become particularly simple if rewritten in polar coordinates centered at $G=(1,0)$. Defining: $$ 1-x=r\cos\theta,\quad -y=r\sin\theta, $$ we obtain: $$ \begin{align} &{dr\over dt}=-v+\omega\sin\theta,\\ &{d\theta\over dt}=-\omega +{\omega\over r}\cos\theta.\\ \end{align} $$ By dividing the first equation by the second, one gets a single equation for the path: $$ {dr\over d\theta}={c-\sin\theta\over 1-(1/r)\cos\theta}, \quad\hbox{where:}\quad c={v\over \omega}. $$ This equation, with the initial condition $r(0)=1$, gives dog's path in the rotating frame.