54

I need help to answer the following question:

Is it possible to place 26 points inside a rectangle that is $20\, cm$ by $15\,cm$ so that the distance between every pair of points is greater than $5\, cm$?

I haven't learned any mathematical ways to find a solution; whether it maybe yes or no, to a problem like this so it would be very helpful if you could help me with this question.

Jack D'Aurizio
  • 361,689
Aryan Patel
  • 499
  • 4
    Do you know the pigeonhole principle? https://en.wikipedia.org/wiki/Pigeonhole_principle – md2perpe Jun 11 '17 at 21:59
  • @jwg, the question was asked to know if it's meaningful to refer to the pigeonhole principle. – md2perpe Jun 12 '17 at 15:06
  • Fair enough @md2perpe, sorry. – jwg Jun 12 '17 at 15:41
  • 2
    seems to me you can only fit 20, and that using the edge (ie, not "inside" the rectangle) and distance being greater or equal to 5, instead of only "greater than". The problem with the 2.5cm radius circle area being larger than rectangle area idea is that a dot on edge will have half its area inside rectangle, and a dot on corner only a quarter, so you cant just sum up area. – Tuncay Göncüoğlu Jun 13 '17 at 11:48
  • @TuncayGöncüoğlu: it looks to me that to prove we cannot fit $21$ points in the given rectangle is extremely difficult. Have you really managed to do it in full rigor? – Jack D'Aurizio Jun 13 '17 at 11:55
  • @JackD'Aurizio cant say I have, tho my main point (I hope) was to express the problem with circle areas, as the illustration clearly shows top in the answer. To prove/disprove, I'm thinking of a "tramboline" figure. give me min :) – Tuncay Göncüoğlu Jun 13 '17 at 11:59
  • @TuncayGöncüoğlu: through circle areas we may show we cannot fit $25$ or $26$ points. The technique has to be severely modified to prove something stronger. The area of $24$ circles with radius $2.5,cm$ is way less than the area of a $(20+5),cm\times (15+5),cm$, and I do not get which "tramboline" you are referring to. – Jack D'Aurizio Jun 13 '17 at 12:10
  • @JackD'Aurizio yep, youre right, doesnt work. My idea was to form a triangle on bottom left edge with a "moving" top, so that as the left bottom corner angle approaches zero, keeping distance to next point towards right over 5. in effect calculating the height of that triangle, and since that triangle will be repeated on next row (in reverse), finding the maximum number of rows that fit in 15cm (and since with every change of angle, total height will be a compound of a single triangles height: hence "tramboline"). – Tuncay Göncüoğlu Jun 13 '17 at 12:34
  • @JackD'Aurizio That height can be calculated as (a=5) => h = a * sqrt(2) / 2 => 3.5355, which gives 4.24 rows, so doesnt really provide extra space for another row, and even reduces dots on even numbered rows. resulting in 18 dots. so.. as I said, doesnt work. – Tuncay Göncüoğlu Jun 13 '17 at 12:35
  • 1
    Let's eliminate the Car Talk Puzzler obfuscation and try to put 26 points in a 3cm by 4cm rectangle that are all at least 1 cm apart. – Spencer Jun 14 '17 at 02:17
  • If the solution sketched in my answer is intended, then the 5x scaling is not obfuscation but rather the reverse. – Gareth McCaughan Jun 14 '17 at 16:14

3 Answers3

109

No, it is not. If we assume that $P_1,P_2,\ldots,P_{26}$ are $26$ distinct points inside the given rectangle, such that $d(P_i,P_j)\geq 5\,cm$ for any $i\neq j$, we may consider $\Gamma_1,\Gamma_2,\ldots,\Gamma_{26}$ as the circles centered at $P_1,P_2,\ldots,P_{26}$ with radius $2.5\,cm$. We have that such circles are disjoint and fit inside a $25\,cm \times 20\,cm$ rectangle. That is impossible, since the total area of $\Gamma_1,\Gamma_2,\ldots,\Gamma_{26}$ exceeds $500\,cm^2$.

enter image description here

Highly non-trivial improvement: it is impossible to fit $25$ points inside a $20\,cm\times 15\,cm$ in such a way that distinct points are separated by a distance $\geq 5\,cm$.

enter image description here

Proof: the original rectangle can be covered by $24$ hexagons with diameter $(5-\varepsilon)\,cm$. Assuming is it possible to place $25$ points according to the given constraints, by the pigeonhole principle / Dirichlet's box principle at least two distinct points inside the rectangle lie in the same hexagon, so they have a distance $\leq (5-\varepsilon)\,cm$, contradiction.

Further improvement: enter image description here

the depicted partitioning of a $15\,cm\times 20\,cm$ rectangle $R$ in $22$ parts with diameter $(5-\varepsilon)\,cm$ proves that we may fit at most $\color{red}{22}$ points in $R$ in such a way that they are $\geq 5\,cm$ from each other.

leo
  • 10,769
Jack D'Aurizio
  • 361,689
  • +1 for the circle area exceeds the available area method! We always used to divide the shape into some holes and consider the points as pigeons seated in the holes. – AHB Jun 12 '17 at 05:10
  • As the OP hasn't "learned any mathematical ways to find a solution", it would be good to include the reason for choosing hexagons. – ShadSterling Jun 12 '17 at 13:56
  • 1
    I find your use of (5−ε) confusing, and I think it's unnecessary; it should be enough to show that the hexagonal tessellation from any corner (which provides the optimal packing of points) will fill the rectangle with less than 26 hexagons. – ShadSterling Jun 12 '17 at 14:01
  • 1
    The reason for choosing hexagons is that an hexagonal tiling gives an optimal circle packing in the plane, if we do not have further constrains. But as you can see, constraints matter a lot: the last modified pentagonal tiling proves a better bound for the current problem, and the optimal packing in the given rectangle is probably a square packing. – Jack D'Aurizio Jun 12 '17 at 14:02
  • "the hexagonal lattice is the densest of all possible circle packings" -- https://en.wikipedia.org/wiki/Circle_packing#Packings_in_the_plane; the only cases where hex tiling is not optimal are where the circles are not all the same size or where the surface is not a plane. – ShadSterling Jun 12 '17 at 18:09
  • 3
    @Polyergic: without additional constraints: a rectangle is not the whole plane. The hexagonal lattice is clearly non-optimal in a $2\times 2$ square, for instance. You can fit $9$ points with mutual distances $\geq 1$ with a square lattice, way less with an hexagonal lattice. – Jack D'Aurizio Jun 12 '17 at 18:18
  • 2
    @Polyergic: the wild behaviour of the constrained problem is pretty clear from this Wikipedia page (https://en.wikipedia.org/wiki/Circle_packing_in_a_square) - sometimes the optimal packing is close to a square packing, sometimes it is closer to an hexagonal packing. – Jack D'Aurizio Jun 12 '17 at 18:22
  • 6
    I find the first part of the answer dubious. The total area of the circles doesn't matter because only their centers need to be inside the rectangle. Using that argument, you can't place 4 points inside a 5x5 square, because the area of 4 circles exceeds 25cm^2. But actually you can just place a point at each corner. – Andre Jun 13 '17 at 14:01
  • 2
    @Andre: this answer works as it is. If you like to use a different argument for proving something else, feel free to do it, but there isn't anything dubious in the first part. $26$ disjoint circles with total area $\geq 510,cm^2$ cannot fit in a $500,cm^2$ rectangle (that, again, is the area of an enlarged rectangle, not the original one), that is all I am saying. – Jack D'Aurizio Jun 13 '17 at 14:03
  • 1
    You can place $4$ points in a $5\times 5$ square, because the area of four circles is less than $(5\color{red}{+5})^2,cm^2$. – Jack D'Aurizio Jun 13 '17 at 14:06
  • 4
    Yes, you are correct. I have overlooked that you are talking about an enlarged area, which is crucial to the argument. Thanks for the clarification. – Andre Jun 13 '17 at 14:10
  • 1
    Hmm... Let's make it a golden answer. :-P – Vidyanshu Mishra Nov 01 '17 at 14:51
107

Jack D'Aurizio's answer is nice, but I think the following is probably the solution intended by whoever posed the puzzle:

Note that $26=5^2+1$. So perhaps we can divide our $20\times15$ rectangle into $5^2$ pieces, apply the pigeonhole principle, and be done. That would require that our pieces each have diameter at most 5. Well, what's the most obvious way to divide a $20\times15$ rectangle into $5^2$ pieces? Answer: chop it into $5\times5$ rectangles, each of size $4\times3$. And lo, the diagonal of each of those rectangles has length exactly 5 and we're done.

Gareth McCaughan
  • 5,030
  • 3
    pretty damn nifty! – Fattie Jun 12 '17 at 12:54
  • This was a great answer for me but probably too terse for the OP (it was too terse for t c who lacked the reputation to ask in a comment). – Carsten S Jun 12 '17 at 14:54
  • 25
    For those who did not immediately understand this: Since the diagonal of the small rectangles has length 5, any two points placed anywhere inside such a rectangle have distance at most 5. Now if we are placing 26 points then at least two of them have to be in the same rectangle (since there are only 25 of them) and hence violate the requirement of having greater than 5. – Carsten S Jun 12 '17 at 14:57
  • If you tile the rectangle with 5cm equilateral triangles, starting with a triangle's corner in bottom left corner of rectangle, (and with half equilateral triangles along the left and right sides), then there are 26 lattice points, 5 on bottom, then 6, then 5, then 6. This doesn't represent a solution, because the end points of the rows of 6 are only 2.5cm from their left/right neighbors and $5\sqrt{3}\over 2$cm from their vertical neighbors. But it could also explain the significance of 26 in the problem. – Χpẘ Jun 12 '17 at 18:20
  • @CarstenS Thanks, I thought the poster was saying it was possible. I was like... no. – Tony Ennis Jun 12 '17 at 22:57
  • 1
    @Χpẘ I think the significance of 26 is that it is one more than 25 and you can partition the area into 25 sections in which if two points are in the same section then they must be within 5cm of each other. If the question asked for 25 points then you wouldn't be able to use this particular argument because you can easily place 25 points in 25 sections with just one point in a section. – Dason Jun 13 '17 at 12:43
  • @Χpẘ that couldn't be it, because "here's a solution that doesn't work" is not proof that there is no solution. – alexis Jun 13 '17 at 14:36
  • 1
    Yes, I don't understand how following the "most obvious" way to slice up the space, and failing to achieve the outcome, demonstrates that there is no other way to achieve the outcome. Surely you need the optimal packing strategy? – Steve Bennett Jun 14 '17 at 01:25
  • 1
    Steve, I think you are misunderstanding (my fault, no doubt, for being too terse). By following the most obvious way to slice up the space, I prove that any way of choosing points must fail to keep them all 5 units apart -- because there are 25 boxes and 26 points, so two must be in the same box, and the boxes have diameter 5 units. The division into boxes is under our control; it's the choice of points that needs to be arbitrary, and so it is. – Gareth McCaughan Jun 14 '17 at 10:50
  • (Sorry, that should say "keep them all >5 units apart".) – Gareth McCaughan Jun 14 '17 at 11:02
2

Although the conclusion is correct, the reasoning in this answer is not. The premise I started from does not apply to the question asked.

(After not finding any apparent community standard for what to do with this sort of incorrect answer, I decided to leave it in place - so that no-one else will duplicate it, and to preserve whatever value it may have, - but with the above note to prevent confusion.)

tl-dr; No.

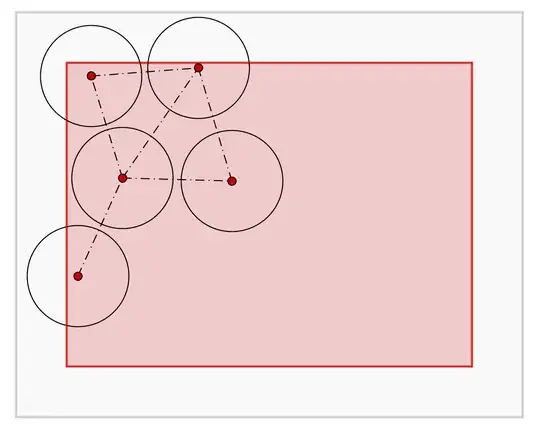
This can be thought of as a circle packing question: treat each point as the center of a circle, and the distance no greater than constraint becomes a circles don't overlap constraint. (It's a little different from the usual "how many circles will fit", because this question is "how many circle-centers will fit" with the rest of each circle allowed to stick out of the rectangle.)

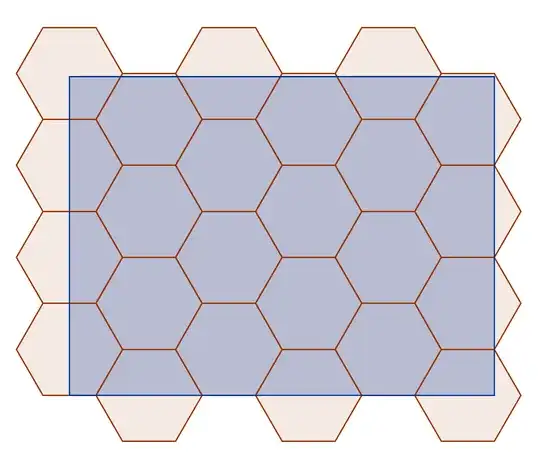
The densest packing of circles that don't overlap is the hexagonal tiling, where each circle is contained by (or inscribed in) a hexagon. (The description where center of each circle is also the center of a hexagon, and the centers of the nearest neighboring circles are the vertices of that hexagon, gives the same arrangement of circles but with larger hexagons; The following may be easier to understand with non-overlapping hexagons.)

The question can be restated as: At a 5cm spacing, will 26 hexagon centers fit inside a 20×15cm rectangle?

We can start by putting one in a corner; this might not be necessary, but it covers the minimum area within the rectangle so there's no better starting point.

Since the hex tiling has straight lines at minimum spacing, we can put a line of points along an edge of the rectangle - along the 20cm edge we can put 5 points (the last of which is on another corner).

Alongside that first line of hexagons we can put another line of hexagons, also spaced 5cm from eachother, which will be $\frac{5\cdot\sqrt{3}}{2} \approx 4.33$cm away from the first line. (Because that's the height of an equilateral triangle with 5cm sides, and the points in the second line are necessarily positioned to make equilaterial triangles with the points in the first line.)

With that line spacing, after the initial line, $\left \lfloor\frac{15\cdot2}{5\cdot\sqrt{3}}\right\rfloor=\left\lfloor\frac{15}{4.33}\right\rfloor=\left\lfloor3.36\right\rfloor=3$ more lines of hexagons will have some centers within the rectangle. Because of the positions of the centers along the lines, they will alternate having 5 and 4 centers within the rectangle.

So the total number of centers within the rectangle will be $5+4+5+4=18$. But that might not be a maximum; it might be possible to get more with a different orientation.

The obvious next orientation to try is with the first line along the 15cm side: $\left\lfloor\frac{20}{4.33}\right\rfloor=\left\lfloor4.62\right\rfloor=4$, so the total number of centers within the rectangle this way will be $4+3+4+3+4=18$.

Is there another orientation that could fit more? The diagonal of the rectangle is $\sqrt{20^2+15^2}=25$, just enough to fit 6 centers along the diagonal. The height of the 15-20-25 triangles on each side is 12cm, so there is room for 2 lines on either side of the diagonal. The first line on each side partitions off a similar triangle with $\frac{12-4.33}{12}\approx0.64$ of the height, so it has a base of $0.64\times25\approx15.98$, so at most 4 centers can be on each of those lines. The second line on each side partitions off a similar triangle with $\frac{12-2\cdot4.33}{12}\approx0.28$ of the (original) height, so it has a base of $0.28\times25\approx6.96$, so at most 2 centers can be on each of those lines. Without considering alignment this gives an upper bound, the maximum number of centers within the rectangle this way is $2+4+6+4+2=18$.

This is not a rigorous proof, but it's enough to convince me. With a minimum distance of exactly 5cm, only 18 points can fit into the rectangle, so with all distances strictly greater than 5cm it is not possible to place 26 points.

ShadSterling
  • 351
  • This is so much lower than the other answer that I fear I've missed something obvious. I'd appreciate it if anyone can point out what. – ShadSterling Jun 13 '17 at 21:33
  • 2
    For one thing the densest packing of circles that don't overlap is the hexagonal tiling doesn't apply here. This is only true in the infinite plane, not necessarily so in a bounded polygon. See e.g. Circle packing in a square for examples of optimal packings which are not based on hexagonal tiling. – dxiv Jun 13 '17 at 21:43
  • @dxiv, that link is about "how many circles will fit", not "how many circle-centers will fit" – ShadSterling Jun 13 '17 at 21:45
  • 1
    That's immaterial, and the same objection holds in both cases. Besides, you started your answer by invoking the densest packing of circles argument. I suggest you read Jack D'Aurizio's answer more carefully. – dxiv Jun 13 '17 at 21:50
  • 1
    Notice that this problem is the same as 'how many circles will fit' in a rectangle that is enlarged by the circles's radius on each side (so, a $25\times 20$ rectangle). – Fimpellizzeri Jun 14 '17 at 05:43
  • @dxiv, that answer has been edited significantly since I read it; its first answer does now seem correct, second seems equivalent to mine but with an erroneous diagram and possibly erroneous numbers, and third still lacks enough explanation to be understood. – ShadSterling Jun 14 '17 at 17:09
  • @Fimpellizieri, I hadn't noticed, thanks for pointing it out. Treating it that way, I think finishing my answer would turn it into a variant of D'Aurizio's second answer (leaving out the unnecessary ε's). – ShadSterling Jun 14 '17 at 17:16
  • 1
    The densest packing of circles that don't overlap is the hexagonal tiling - this is still wrong. The claim is true in the plane, not in a generic $n\times m$ rectangle. Additionally, it is pretty trivial that we may put $20$ points at a distance $\geq 1$ from each other in a $3\times 4$ rectangle: it is enough to start from a vertex and follow a square grid. – Jack D'Aurizio Jun 18 '17 at 00:15
  • Ok, I see it now. So what does one do with this sort of wrong answer? – ShadSterling Jun 20 '17 at 00:46