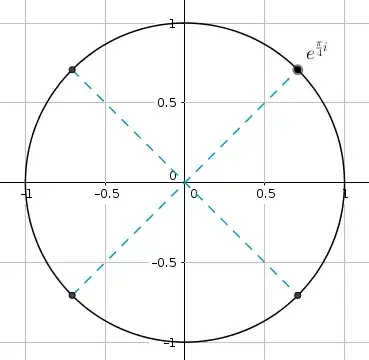
For $z \in \mathbb{C}$, how can I find all roots of the equation $$ z^4 + 1 = 0 $$ Obviously, this equation implies $$ z^4 = -1 = e^{i \pi} $$ and thus, one of our roots must be $$ z_1 = e^{\frac{i \pi}{4}} $$
However, I am aware that this is not the only root. How can I find all other roots of this equation?
Actualy you should write
$$z^4=-1=e^{i(\pi+2k\pi)}\to z_k=e^{\frac{i\pi(2k+1)}{4}}$$
Now make $k=0,1,2,3$ and get your roots.
Recall that when you have found the principle $n$-th root of a complex number, the remaining roots are equally spaced about the circle containing the principle root and having center the pole.
In general if $b$ is a solution to $z^n=a$, all the solutions are $b_0=b$, $b_1=b e^{2\pi i/n}$, $b_2=b e^{4\pi i/n},\ldots,b_{n-1}=be^{2(n-1)\pi i/n}$.
If $z=\mathrm e^{i\theta}$, you just have to solve $$4\theta\equiv \pi\mod2\pi\iff\theta\equiv \frac\pi4\mod\frac\pi 2.$$
Alternatively, once you have one $4$th root of a complex number, you obtain all the roots multiplying it by the $4$th roots of unity, i.e. by $1,-1, i,-i$.
