2

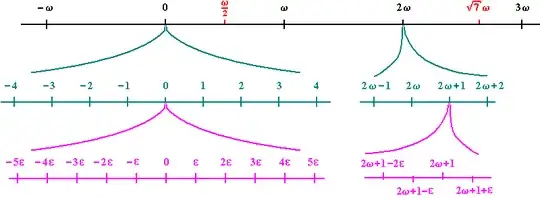
I just found out about the hyperreals. Here is a visualization of the hyperreals:

enter image description here

The problem I have with this image, is that it conveys a very clear intuition, but often times, those intuitions are very misleading, so I don't know exactly how to interpret this.

My first idea is that the hyperreals are simply the same as $R^3$ (assuming there are is no fourth "level", as in the image here), because when we add $a\omega +b$ to $c\omega + d$, we get $(a+c)\omega + (b+d)$, just as if we added two vectors. If we multiply a hyperreal by a real number, we multiply both components.

It seems like the only addition that the hyperreals have, is an order. specifically it is a lexicographic order.

Am I correct that the hyperreals are simply $R^3$ with a lexicographic order? What's so special about them?

Bonus question: What is the difference between the hyperreals and the surreal numbers?

Community
  • 1
user56834
  • 12,323
  • 1
    There is a fourth level. And a fifth. And a sixth. ... It extends infinitely in both directions. For example $\varepsilon^2$ and $\omega^2$ are both beyond your picture, – M. Winter May 22 '17 at 09:12
  • What operation do we have to do to get from $a\omega +b$ to $c\omega^2+d\omega+e$? My impression is that ${a\omega + b |a,b\in \mathbb R}$ is closed under arithmetic operations? In any case, if it is not closed, can't we still consider it as $\lim_{n\to \infty}\mathbb R^n$, so that my idea holds? – user56834 May 22 '17 at 09:24
  • 1
    You get there by multiplication. You have $(a\omega+b)(c\omega+d)=ac\omega^2+(a+c)\omega+bd$. $\lim_{n\to\infty}\Bbb R^n$ might come closer as the hyperreals are defined as equivalence classes of real valued functions anyway (as far as I remember). See here – M. Winter May 22 '17 at 09:27

1 Answers1

1

For bonus question.

The hyperreals (a "baby" name for nonstandard models of $\mathbb R$) have additional information: the transfer principle.

The surreals have addional information: simplicity (a technical notion, some numbers are "simpler" than others).

They are both nonarchimedean ordered fields containing the reals ... and all nonarchimedean ordered fields containing the reals admit structure such as you illustrate in your pictures.

There are others, too. Levi-Civita numbers. And (plug) transseries

G. Edgar, Transseries for beginners, Real Analysis Exchange 35 (2010) 253--310

egreg
  • 244,946
GEdgar
  • 117,296