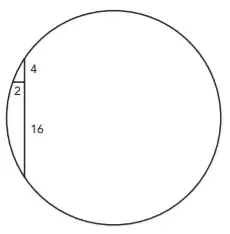
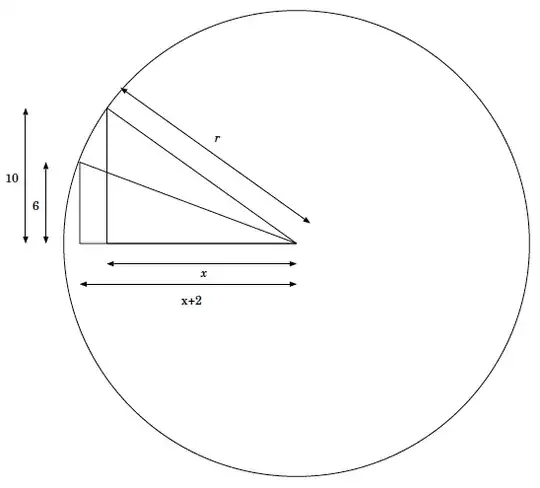
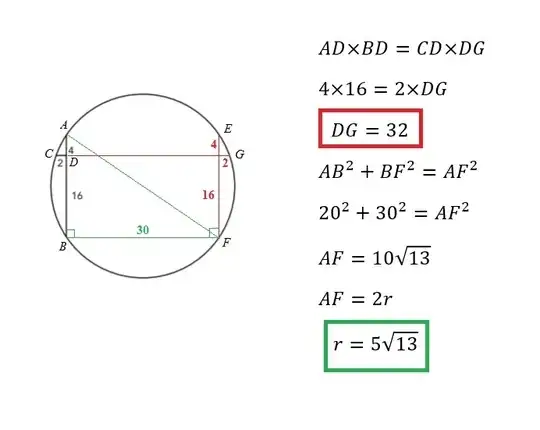
It looks like a simple question, but for some reason I just can't figure out how to do it: I am given the following circle (see picture) and need to calculate the radius. I know how this works when you know the chord height, but not when you are given line segments as shown.
Thanks in advance.
Use the Law of sines
Let $R$ the circumradius of the triangle $ABC$ \begin{align*} \frac{|AC|}{\sin B}&=2R\\[4pt] \frac{\sqrt{2^2+4^2}}{\frac2{\sqrt{2^2+16^2}}}&=2R\\[4pt] \frac{\sqrt{20}\sqrt{260}}{2}&=2R \end{align*}
Then $R=5\sqrt{13}$.
Basic approach. Draw two right triangles, and equate their hypotenuses to the radius:
Use the Pythagorean theorem. Drawing is approximately but not perfectly to scale.
Consider the function $$y=\sqrt{r^2-(x-10)^2}+b$$ This defines the upper arc of a circle centred on $(10,b)$ with radius $r$. We want it to touch $(0,0)$ and $(0,20)$, and setting the equation up at either of these points yields the same result: $$0=\sqrt{r^2-100}+b$$ $$b^2=r^2-100\tag1$$ Now we are given that $(16,2)$ is on the arc: $$2=\sqrt{r^2-36}+b$$ $$(2-b)^2=4-4b+b^2=r^2-36\tag2$$ Subtract $(1)$ from $(2)$: $$4-4b=64\qquad b=-15$$ Now the radius $r$ comes easily: $$r=\sqrt{b^2+100}=5\sqrt{13}$$
