Why is the affine line with a doubled point not a separated scheme?

Question

How to show, that the affine line with a split point is not a separated scheme? Hartshorne writes something about this point in product, but it is not product in topological spaces category! Give the most strict proof!

Answer 1

Let $X$ be the affine line with the origin doubled. More precisely, if we let $Z = \mathbb A^1$ and $U = \mathbb A^1 \setminus \{0\},$ then $X$ is the union of two copies of $Z$ in which the two copies of $U$ are identified in the obvious way. There are two obvious maps $Z \to X$ (corresponding to the two copies of $Z$ of which $X$ is the union), and they are distinct, but they coincide when restricted to $U$.

These two maps induce a map $Z \to X \times X$, and the above discussion shows that preimage of the diagonal is exactly equal to $U$. Since $U$ is not closed in $Z$, we conclude that the diagonal is not closed in $X\times X$. Thus $X$ is not separated.

Answer 2

Let $X$ be the affine line with a doubled origin. By definition, $X$ is constructed by gluing two schemes $V_1 = \text{Spec }k[t]$, $V_2 = \text{Spec }k[u]$ (which we subsequently identify with open sets of $X$) along the open set $U \subset X$ isomorphic to $\mathbb{A}^1\setminus \{0\}$ via the isomorphism $k[t, 1/t] \cong k[u, 1/u]$ defined by $t \leftrightarrow u$. The fibered product $X\times_k X$ is then covered by the open sets $V_1 \times_k V_1$, $V_2 \times_k V_2$, $V_1\times_k V_2,$ and $V_2\times_k V_1$.

Since $\mathbb{A}^1 \times_k \mathbb{A}^1 \cong \mathbb{A}^2$, we see that each of these open sets $V_i \times_k V_j$ is isomorphic to $\mathbb{A}^2$, and that $X$ is obtained from these sets by gluing appropriately. As a result, to compute the image of $\Delta_X : X \to X\times_k X$, it is enough to compute $\Delta_X(V_1)$ and $\Delta_X(V_2)$. We see that $\Delta_X(V_1)$ contains the origin in $V_1 \times_k V_1$ and $\Delta_X(V_2)$ contains the origin in $V_2 \times_k V_2$, while neither $\Delta_X(V_1)$ nor $\Delta_X(V_2)$ contains the origins in $V_1 \times_k V_2$ or $V_2 \times_k V_1$. (Indeed, by computing these fibered products locally, we see for example that $\Delta_X(V_1) \cap V_1 \times_k V_1$ is isomorphic to $\mathbb{A}^1$ sitting in the diagonal of $\mathbb{A}^1\times_k \mathbb{A}^1$, while $\Delta_X(V_1) \cap V_1 \times_k V_2$ is isomorphic to $\mathbb{A}^1 \setminus \{0\}$ sitting in the diagonal of $\mathbb{A}^1\times_k \mathbb{A}^1$.)

This is what is meant by the comment above stating that $X\times_k X$ has "four origins" while $\Delta_X(X)$ contains only two of them. From here, Matt's answer tells us that the subset $\Delta_X(X) \subset X\times_k X$ containing "two origins" is not closed in $X\times_k X$, and so $X$ is not separated over $k$.

Answer 3

I just want to give a little more of justification and clarification of Matt's excellent answer from a more scheme-theoretical point of view.

By definition, we want to show that the diagonal morphism $X\longrightarrow X\times_k X$ is not a closed embedding. To show this, you need to know, first, the diagonal morphism is always a locally closed embedding, which means that it's a closed embedding if we core strict the diagonal morphism to a open subscheme of $X\times_k X$, you can find the proof here.

Then, we need the fact that a locally closed embedding whose image is closed is a closed embedding, you can find the proof here.

Therefore, we only have to show that the image of the diagonal morphism is not closed(This is what Matt's Answer is talking about). And the way will do it is we will establish a morphism $\pi:\mathbb{A}^1_k\longrightarrow X\times_k X$ such that the inverse image of the diagonal is not closed, where we need to do some computations involving fiber products, which is a good exercise illustrating how we generally deal with these kind of computations locally.

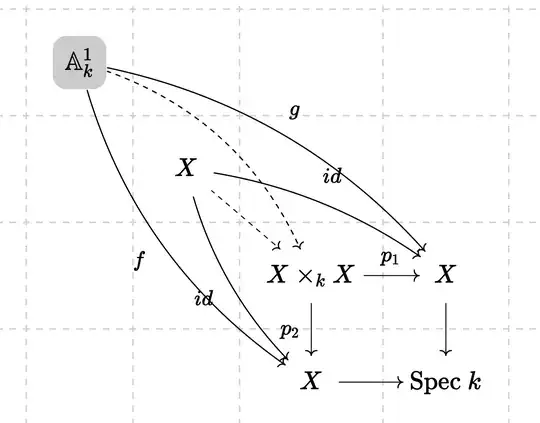
Suppose that we are working over any field $k$, let $\mathbb{A}^1_k=Speck[t]$ be the affine line and $X$ be the affine line with double origins obtained by gluing two $\mathbb{A}^1_k$ together along the identity morphism in $D(t)$. We will call the two copies of $\mathbb{A}^1_k$ in $X$ $A_1$ and $A_2$ for simplicity. Consider the following diagram where dotted arrows are induced by universal property of fiber products, the induced map from $\mathbb{A}^1_k$ to $X\times_k X$ will be $\pi:\mathbb{A}^1_k\longrightarrow X\times_k X$ we mentioned before:

Here $f,g$ are defined to be the maps $\mathbb{A}^1_k$ to the two distinct copies $A_1$ and $A_2$ in $X$. It's an exercise to check that this definition makes the diagram commutative (just use the fact the global section of X $k[t]$ and morphisms of affine schemes are determined by the associated ring maps between their global sections). Then standard computation following the construction of fiber product shows that the image of the diagonal map is $A_1\times_k A_1 \cup A_2\times_k A_2$ is $D(t)$ in $\mathbb{A}^1_k$. Then we take the inverse image which is $\pi^{-1}(A_1\times_k A_1)\cup \pi^{-1}(A_2\times_k A_2)$.

The computation to compute the inverse image is a little bit cumbersome, the general ideal is that since $f,g$ maps the affine line to two distinct copies in $X$, following the construction of morphisms to fiber product induced by the universal property, we find the inverse image $\pi^{-1}(A_1\times_k A_1)$ will be of the form $D(t)\cap \mathbb{A}^1_k=D(t)$ so is $\pi^{-1}(A_2\times_k A_2)$, this is what we want, since $D(t)\subset \mathbb{A}^1_k$ is a dense open, not closed!