$\def\d{\mathrm{d}}$Determine the integral $$\oint_L \mathbf{A} \cdot \,\d\mathbf{r},$$ where $$\mathbf{A} = \mathbf{e}_x(x^2-a(y+z))+\mathbf{e}_y(y^2-az)+\mathbf{e}_z(z^2-a(x+y)),$$ and $L$ is the curve given by the intersection between the cylinder $$\begin{cases}(x-a)^2+y^2=a^2 \\z\geq0\end{cases}$$ and the sphere $$x^2+y^2+z^2=R^2, \quad (R^2>4a^2)$$ The orientation is such that at $x=0$ the tangent to the curve is parallel with $-\mathbf{e}_y$.
Attempted solution:
Let's apply Stokes' theorem. First, let me introduce a graphical representation of the problem.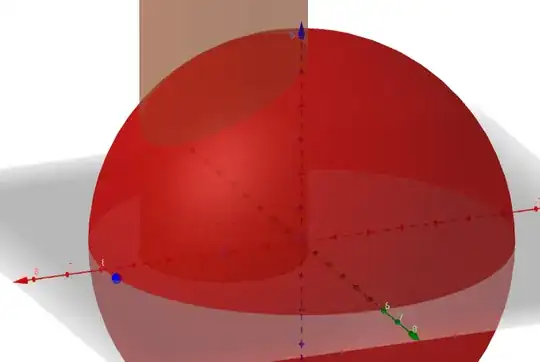 The path $L$ will then, as seen from above, be the following:
The path $L$ will then, as seen from above, be the following: 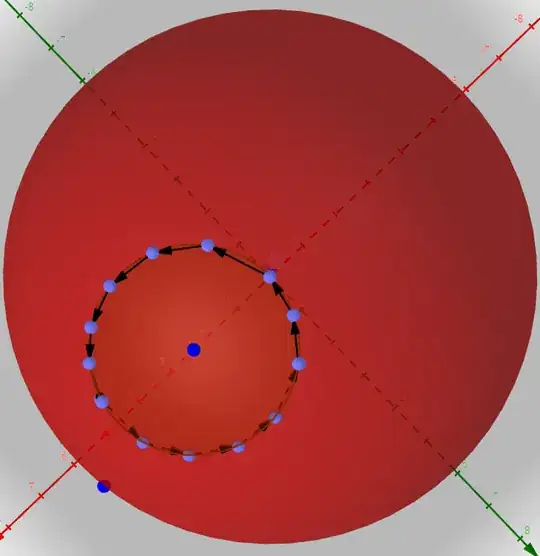
A simple calculation shows $\nabla \times \textbf{A} = (0,0,a)$. Here comes my problem...
Question
What surface am I looking to take a surface integral over? Is it the whole cylinder or just the "top"? How can I determine?