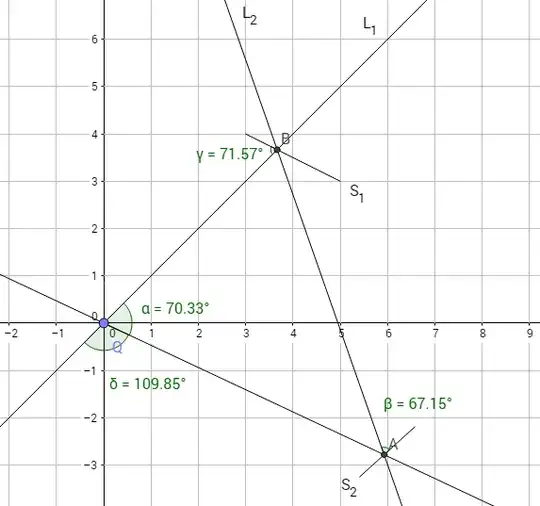
Understanding a Theorem on Rotations as the Product of Reflections

Question

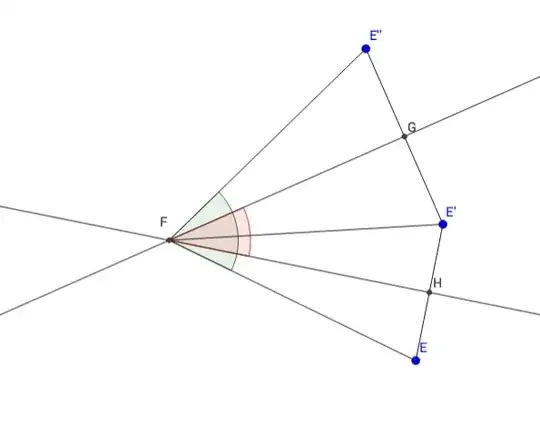
I'm currently having trouble understanding this theorem, discussing reflections in a 2D plane:

Theorem: If we perform a reflection $S_1$ about a line $l_1$ followed by a reflection $S_2$ about the line $l_2$, the resulting transformation is a rotation about the point of intersection Q of the two lines. The rotation is from the line $l_1$ to the line $l_2$, and by an angle $2 \theta$, where $\theta$ is the angle between the two lines.

Here's what I thought it meant, note that the angles of reflection are approximated, mostly due to never using GeoGebra before.

Anyways, it's looks somewhat clear that adding $\gamma+ \beta $ doesn't give either $\alpha$ nor $\delta$. Is there something I'm missing? If I made $\gamma= \beta$, would it then be the case that either $\gamma + \beta = \alpha$ or $\gamma+\beta = \delta$?

For the meaning of that statement see the animation in an old answer of mine. The angle between the black and orange arrows is always twice the angle between the two lines. — Jyrki Lahtonen, Apr 15 '17 at 13:16

score 3 · Accepted Answer · answered Apr 15 '17 at 13:24

The figure represents the situation of the theorem.

The point $E$ ir reflected at $E'$ than at $E''$. The transformation $E \to E''$ is a rotation around the point $F$ by an angle $ \angle EFE''$ tha is double the angle $\angle GFH$ between the two lines because the triangles $EFE'$ and $E'FE''$ are isosceles.

Understanding a Theorem on Rotations as the Product of Reflections

1 Answers1

Linked