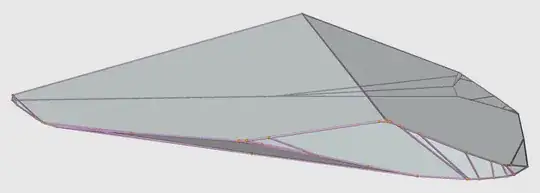
The images of $\left(\frac{427}{6984}, \frac{761}{6984}, \frac{1421}{6984}\right)$ under $I4_132$ indeed generate this polyhedron as their Voronoi cells. I used this description of $I4_132$ and wrote the Python program below that outputs the polyhedron’s vertices and faces in OFF format. As expected, it has 70 vertices, 38 faces, and 106 edges.
import itertools
import numpy as np
import scipy.spatial
# generating point from https://refubium.fu-berlin.de/handle/fub188/10176
x0, y0, z0 = 427 / 6984, 761 / 6984, 1421 / 6984
# I4₁32 from https://stevedutch.net/symmetry/3dspacegrps/3dspgr212-214.htm
other_points = [
(x2 + i, y2 + j, z2 + k)
for x1, y1, z1 in [
(x0, y0, z0),
(x0 + 1 / 2, y0 + 1 / 2, z0 + 1 / 2),
]
for x2, y2, z2 in [
(x1, y1, z1),
(x1, -y1, 1 / 2 - z1),
(1 / 2 - x1, y1, -z1),
(-x1, 1 / 2 - y1, z1),
(z1, x1, y1),
(-z1, 1 / 2 - x1, y1),
(z1, -x1, 1 / 2 - y1),
(1 / 2 - z1, x1, -y1),
(y1, z1, x1),
(1 / 2 - y1, z1, -x1),
(-y1, 1 / 2 - z1, x1),
(y1, -z1, 1 / 2 - x1),
(3 / 4 + x1, 3 / 4 - z1, 1 / 4 + y1),
(1 / 4 + x1, 3 / 4 + z1, 3 / 4 - y1),
(1 / 4 - x1, 1 / 4 - z1, 1 / 4 - y1),
(3 / 4 - x1, 1 / 4 + z1, 3 / 4 + y1),
(1 / 4 + z1, 3 / 4 + y1, 3 / 4 - x1),
(3 / 4 - z1, 1 / 4 + y1, 3 / 4 + x1),
(1 / 4 - z1, 1 / 4 - y1, 1 / 4 - x1),
(3 / 4 + z1, 3 / 4 - y1, 1 / 4 + x1),
(3 / 4 - y1, 1 / 4 + x1, 3 / 4 + z1),
(3 / 4 + y1, 3 / 4 - x1, 1 / 4 + z1),
(1 / 4 - y1, 1 / 4 - x1, 1 / 4 - z1),
(1 / 4 + y1, 3 / 4 + x1, 3 / 4 - z1),
]
for i in range(int(x0 - x2 - 1.001), int(x0 - x2 + 2.001))
for j in range(int(y0 - y2 - 1.001), int(y0 - y2 + 2.001))
for k in range(int(z0 - z2 - 1.001), int(z0 - z2 + 2.001))
if (x2 + i, y2 + j, z2 + k) != (x0, y0, z0)
]
hs = scipy.spatial.HalfspaceIntersection(
np.array(
[
[
2 * (x1 - x0),
2 * (y1 - y0),
2 * (z1 - z0),
(x0 + x1) * (x0 - x1) + (y0 + y1) * (y0 - y1) + (z0 + z1) * (z0 - z1),
]
for x1, y1, z1 in other_points
]
),
np.array([x0, y0, z0]),
)
faces = []
for dual_facet in set(sum(hs.dual_facets, [])):
adj = {}
for i, j in itertools.combinations(
(i for i in range(len(hs.dual_facets)) if dual_facet in hs.dual_facets[i]), 2
):
if set(hs.dual_facets[i]) & set(hs.dual_facets[j]) - {dual_facet}:
adj.setdefault(i, []).append(j)
adj.setdefault(j, []).append(i)
start = a = min(adj)
b = min(adj[a])
face = [a]
while b != start:
a, [b] = b, set(adj[b]) - {a}
face.append(a)
faces.append(face)
print("OFF")
print(len(hs.dual_facets), len(faces), sum(map(len, faces)) // 2)
for vertex in hs.intersections:
print(*vertex)
for face in faces:
print(len(face), *face)
Try it online!
