How to find LCM of two numbers when one starts with an offset

Question

In the world of natural numbers,

a RED and a GREEN guy start from 0 and walk down the numberline. If the RED guy moves in steps of size r and the GREEN guy moves in steps of size g, the spots on the numberline where both will step are k * lcm(r, g) where k is a natural number.

How to find such spots in case when GREEN guy starts with an advantage of a?

Answer 1

(This answer is based on fleablood's answer and provides more details on how exactly to compute the result. Also, I have renamed some variables from the question to make the answer IMO easier to follow in isolation but hopefully the mapping is clear.)

Math

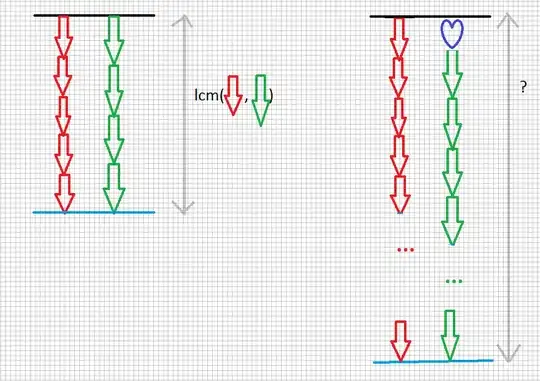
Assume that we have two periodic systems $A$ and $B$ with periods $p_A$, $p_B$ and phases $\phi_A$, $\phi_B$. I found that it was mathematically simplest to take "phase" to mean the number of steps past the most recent reference point. So in the question: steps are y-axis ticks, the arrow lengths are the periods, the ends of the arrows are reference points, and the phase of the second arrow is the negative advantage (since advantage measures steps-to-go from the origin to the next reference point rather than steps completed so far).

It takes time $p_A - \phi_A$ to visit the reference point of $A$ for the first time and additional time $p_A$ after that. So the time after visiting the reference point of $A$ $m$ times is $m \cdot p_A - \phi_A$.

We want to find a time where $A$ and $B$ are both at their reference points, so we want $m$, $n$ such that $m \cdot p_A - \phi_A = n \cdot p_B - \phi_B$. We don't have to worry about this being non-negative or minimal because we know that the combined period of $(A, B)$ is $p_C = \mathrm{lcm}(p_A, p_B)$ so we can just mod by that. Rearrange this to get: $$ m \cdot p_A - n\cdot p_B = \phi_A - \phi_B \tag{1}\label{1} $$

Using the Extended Euclidean Algorithm, we can find values $s$, $t$ such that

$$ s \cdot p_A + t \cdot p_B = g \tag{2}\label{2} \\ \text{ where } g = \mathrm{gcd}(p_A, p_B) $$

If $g$ does not divide $\phi_A - \phi_B$ then we cannot proceed: $A$ and $B$ will never land on their reference points at the same step. Otherwise, multiply (2) by $z = \frac{(\phi_A - \phi_B)}{g}$ to get (1) with $m = z \cdot s$ and $n = - z \cdot t$.

Therefore, $A$ and $B$ are both at the reference points at step $m \cdot p_A - \phi_A$. Take this mod $p_C$ to get the first positive time they coincide: $$ x = (m \cdot p_A - \phi_A) \text{ mod } p_C $$ or in terms of phases: $$ \phi_C = (-m \cdot p_A + \phi_A) \text{ mod } p_C. $$

Python Implementation

def combine_phased_rotations(a_period, a_phase, b_period, b_phase):
    """Combine two phased rotations into a single phased rotation
Returns: combined_period, combined_phase

The combined rotation is at its reference point if and only if both a and b
are at their reference points.
"""
gcd, s, t = extended_gcd(a_period, b_period)
phase_difference = a_phase - b_phase
pd_mult, pd_remainder = divmod(phase_difference, gcd)
if pd_remainder:
    raise ValueError("Rotation reference points never synchronize.")

combined_period = a_period // gcd * b_period
combined_phase = (a_phase - s * pd_mult * a_period) % combined_period
return combined_period, combined_phase



def arrow_alignment(red_len, green_len, advantage):
    """Where the arrows first align, where green starts shifted by advantage"""
    period, phase = combine_phased_rotations(
        red_len, 0, green_len, -advantage % green_len
    )
    return -phase % period
def extended_gcd(a, b):
    """Extended Greatest Common Divisor Algorithm
Returns:
    gcd: The greatest common divisor of a and b.
    s, t: Coefficients such that s*a + t*b = gcd

Reference:
    https://en.wikipedia.org/wiki/Extended_Euclidean_algorithm#Pseudocode
"""
old_r, r = a, b
old_s, s = 1, 0
old_t, t = 0, 1
while r:
    quotient, remainder = divmod(old_r, r)
    old_r, r = r, remainder
    old_s, s = s, old_s - quotient * s
    old_t, t = t, old_t - quotient * t

return old_r, old_s, old_t

print(arrow_alignment(red_len=9, green_len=15, advantage=3))  # 18
print(arrow_alignment(red_len=30, green_len=38, advantage=6))  # 120
print(arrow_alignment(red_len=9, green_len=12, advantage=5))  # ValueError

Answer 2

Let $d = \gcd(Green, Red)$, everystep Green takes will be multiple of $d$ offset by advantage $a$ and every step Red takes will be a multiple of $d$. So $a$ has to be a multiple of $d$ if they are ever to be in synch.

By Euclid's Lemma there exists integers $M,N$ so that $M*Red - N*Green = a$. Find those and have Red and Green take those steps to get a number they will be synched at. Then all multiples of the LCM from there will have them in synch.

===

Example: if G = 15 and R = 9 and a = 3. Then $\gcd(R,G) = 3$ and $2R - G = a$. So R goes forward from zero two steps to 18. and G goes forward from 3 one step to 3+15 = 18. They will be in synch. LCM$(15,9)=45$ so they will be in synch $18 \pm 45k$

or less trivial G = 38 and R = 30 and a=6. $\gcd(G,R) = 2$ and so $38 - 30 = 8$ and $3*8 + 6 = 30$ so $3(38-30)+6 = 30$ so $6= 4*30 - 3*38$. So red goes forward four steps. $0 + 4*30 = 120$ and green goes forward three. $6 + 3*38=6 + 114=120$. LCM$(38,30) = 19*2*15=570$. Then will be in synch $120 \pm 570k$.

Example of failure. Green = 12 and Red = 9 and a = 5. $\gcd(12,9) =3$ and $3\not | 5$. Green will always be on $5 + 12k \equiv 2 \mod 3$ and red will always be on $3j \equiv 0 \mod 3$. They will never synch.