Given the two foci of an ellipse and a tangent line of the ellipse, can one construct the ellipse with a compass and a straightedge?
Asked
Active
Viewed 255 times
1
-
1Using optical property of ellipses. – Ng Chung Tak Apr 03 '17 at 12:45
-
There is a unique ellipse if that is what you mean - if not when would you consider the ellipse constructed and with which instruments? – Martin Rattigan Apr 03 '17 at 13:26
-
@NgChungTak Can you be more specific? – pepa.dvorak Apr 03 '17 at 14:12
-
@MartinRattigan Question specified. – pepa.dvorak Apr 03 '17 at 14:12
-
What do you mean by "construct the ellipse with a compass and a straightedge"? Constructing a point on the ellipse would be enough? Or you need a construction of the four vertices? – Intelligenti pauca Apr 03 '17 at 14:23
-
I didn't understand the comment "Question specified". Ng Chung Tak has posted a method of drawing the ellipse with a piece of string and presumably pins to fix the ends as implements. This may be what you meant by constructing the ellipse in which case I would suggest you accept the answer. Some methods of drawing ellipses are shown here: https://www.uwgb.edu/dutchs/MATHALGO/Ellipses.HTM. There is no method of tracing out exact ellipses by using ruler and compasses in the prescribed manner nor of practicably constructing more than a finite number of points lying on the ellipse. – Martin Rattigan Apr 03 '17 at 15:18
-
Incidentally, for a string and pins method, a loop tightened around pins at $A$ and $B$ and the point $C$ would allow the ellipse to be traced in a single path without the string catching on the pins and may be more practical. – Martin Rattigan Apr 03 '17 at 15:18
1 Answers
6
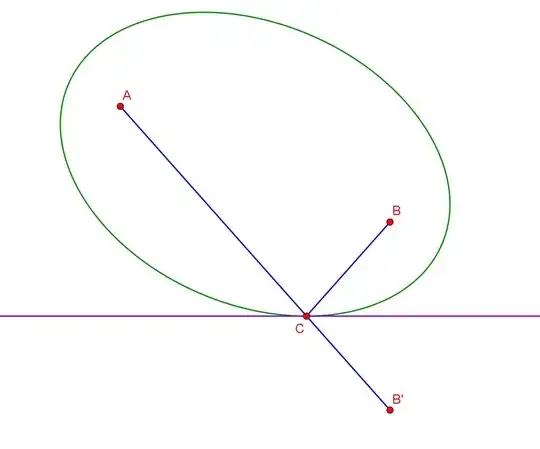
$A$ and $B$ are the two foci, $B'$ is the mirror image of $B$ about the tangent. Now $AB'$ meets the tangent at $C$. Construct the ellipse with string of length $AB'=AC+BC$ with its ends on foci $A$ and $B$.
Ng Chung Tak
- 19,693