How to solve an equation of the form $f(x)=f(a)$ for a fixed real a.

Question

I got stuck on this question: find all solutions $x$ for $a\in R$:

$$\frac{(x^2-x+1)^3}{x^2(x-1)^2}=\frac{(a^2-a+1)^3}{a^2(a-1)^2}$$

I see that if we simplify we get:

$$\frac{(x^2-x+1)^3}{x^2(x-1)^2}=\frac{[(x-{\frac 12})^2+{\frac 34}]^3}{[(x-{\frac 12})^2-{\frac 14}]^2}$$

From the expression $(x-{\frac 12})^2$, I see that if $x=x_1$ is a solution, then $x=1-x_1$ is also a solution. But in the solution to this exercise, it was stated that $x=\frac{1}{x_1}$ must also be a solution, and I don't see how.

[EDIT]

Ok, thx for the help guys. What do you think of this solution (doesn't involve any above precalculus math, and needs no long calculations)?

From the above we know that if $x_1=a$ is a solution, then $x_2=1-a$ is also a solution.

Also, from here:

$$\require{cancel}\frac{(x^2-x+1)^3}{x^2(x-1)^2}=\frac{\cancel{x^3}(x+{\frac 1x}-1)^3}{\cancel{x^3}(x+{\frac 1x}-2)}$$

in the expression $x+{\frac 1x}$ we see that if $x=x_1$ is a solution, then $x=\frac{1}{x_1}$ is also a solution, so $x_3=\frac{1}{a}$.

With these two rules we can now keep generating roots until we have 6 total.

If $x=x_2$ is a solution, then $x=\frac{1}{x_2}$ is also a solution, so $x_4=\frac{1}{1-a}$.

If $x=x_3$ is a solution, then $x=1-x_3$ is also a solution, so $x_5=\frac{a-1}{a}$.

Finally, if $x=x_5$ is a solution, then $x=\frac{1}{x_5}$ is also a solution, so $x_6=\frac{a}{a-1}$

The 6 obtained values are distinct, so they cover all the roots.

[EDIT2]

I guess this is answered. No sure whose particular answer to actually select as the right one since they're all correct, so I'll just leave it like this.

Answer 1

Let $$f(x)=\frac{(x^2-x+1)^3}{x^2(x-1)^2}\tag{1}$$

(representative curve in Fig. 1).

Your question can be reformulated in the following way :

$$\text{for a given} \ a, \ \ \text{find all} \ x \ \text{such that} \ \ f(x)=f(a) \tag{2}$$

This answer will have 3 parts : A) Solving the problem itself, B) Understanding a little the associated group, C) Considering function $f$ in a larger scope.

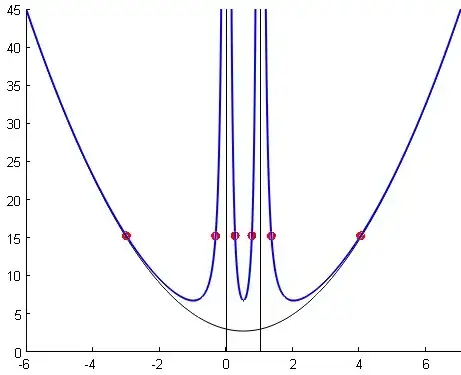
Fig. 1. The red dots correspond to: $f(-3)=f(-1/3)=f(1/4)=f(3/4)=f(4/3)=f(4)=2197/144$ where the values $-3,-1/3,\cdots 4$ are the values $\varphi_k(-3)$ (the first one corresponding to identity function with notations found below). The vertical asymptotes and the asymptotic parabola (with equation $y=x^2-x+3$) are also featured.

A) Solving the problem itself

First of all, the variations of $f$ are easily established once we remark that

$$\tag{3}f'(x)=\underbrace{(x^2-x+1)}_{>0 \ \text{for all} \ x}\dfrac{(x-2)(2x-1)(x+1)}{x^3(x-1)^3}.$$

We deduce from (3) the existence of 3 minima in $(-1,a), (0.5,a)$ and $(2,a)$ where $a=27/4=6.75.$

We can observe (by computations) the following facts, with the introduction of spécific notations

• $f(x)=f(\underbrace{1-x}_{\varphi_2(x)})$.

• $f(x)=f(\underbrace{1/x}_{\varphi_3(x)})$.

In a natural way the composition of these two invariant transforms, $\varphi_3\circ\varphi_2$ and $\varphi_2\circ\varphi_3$, gives rise to a new invariance property :

• $f(x)=f(1-1/x)$ meaning that if $x$ is solution, $a=1-1/x$ is also a solution ; in the same vein :

• $f(x)=f(1/(1-x))$ meaning that if $x$ is solution, $a=1/(1-x)$ is also a solution.

A last invariant transformation :

• $f(x)=f(x/(x-1))$ meaning that if $x$ is solution, $a=x/(x-1)$ is also a solution.

We can summarize all this in the following manner:

$$\tag{4}f(x)=f(\varphi_k(x))$$

for all "homographic" functions belonging to the so-called (6 elements) anharmonic group (in the sense of group theory):

$$\phi_1(x)=x, \ \phi_2(x)=1-x, \ \phi_3(x)=\tfrac{1}{x}, \ \phi_4(x)=1-\tfrac{1}{x}, \ \phi_5(x)=\tfrac{1}{1-x}, \ \phi_6(x)=\tfrac{x}{x-1}.$$

Conclusion : Equation (2) has

• 6 solutions if $a\neq -1,1/2,2$ : $ \ x=a, \ 1-a, \ \tfrac{1}{a}, \ 1-\tfrac{1}{a}, \ \tfrac{1}{1-a}, \ \tfrac{a}{a-1} $

• 3 solutions if $a=-1,1/2,2$ which are... $x=-1,1/2,2$

Are there other transformations that we haven't considered ? No, because for a given $a$, i.e, for a given $b=f(a)$, there are 5 other points of the curve with a common ordinate $b$, not less not more (set apart the special case of the minimal points). But in fact the fundamental interplay between function $f$ and the group just described can only be understood through "higher algebra" considerations that we will see in part C.

Remark : we could have taken profit of the fact that the curve has a symmetry with respect to a vertical axis situated at $x=\dfrac12$. Indeed, setting $x=X+\dfrac12$, we get a new (even) equation simpler than the initial one :

$$Y=\dfrac{(4X^2+3)^2}{4 (4X^2-1)^2}$$

B) Understanding a little the associated anharmonic group

(see (https://en.wikipedia.org/wiki/Cross-ratio))

It can be considered as a (finite) subgroup of $PGL(2,\mathbb{Z})$ through a classical linear representation (in short : representation by matrices) :

$$\dfrac{az+b}{cz+d} \ \ \ \leftrightarrow \ \ \ \begin{pmatrix}a&b\\c&d\end{pmatrix}$$

It is isomorphic to $S_3$, the group of permutation on 3 objects.

It is generated by $\varphi_2$ and $\varphi_3$.

It has a nice vizualization in terms of "fundamental regions":

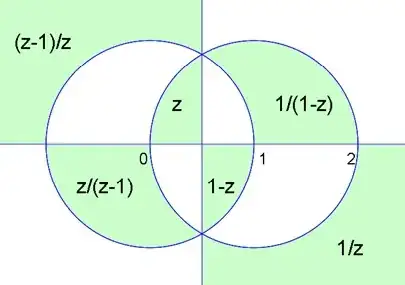
Fig. 2 : if $z$ belongs to the green "triangular" region, then $1-z$ belongs to... etc. Please note that straight line $x=\tfrac12$ is an axis of symmetry like for Fig. 1.

C) Considering function $f$ in a larger scope

Why is this working so well ? Because this is the tip of an iceberg. Indeed, function $f$ is the "Klein j-invariant" (see (https://arxiv.org/pdf/1810.08742.pdf)(https://math.stackexchange.com/q/3418400) (http://www.cis.upenn.edu/~jean/gma-v2-chap5.pdf) exercice 5.14) associated with anharmonic group in projective geometry ; it would be too long to explain it here. See for that the Wikipedia article (https://en.wikipedia.org/wiki/Cross-ratio). This invariant is associated with elliptic curves.

Remarks : other connections : How is $E = S(x)$, where $E = k(x), k$ a field, and S= k(I) of all rationals functions of $I = I(x) = \frac{(x^2 -x+1)^3}{x^2(x-1)^2}$? ; about Lüroth theorem https://upload.wikimedia.org/wikipedia/commons/3/3e/Another_elementary_proof_of_Luroth%27s_theorem-06.2004.pdf ; Klein's invariant and negative discriminant} ; an interesting inequality :https://artofproblemsolving.com/community/c6h1447345p8277143

Answer 2

factorizing the given equation and cancel the denominators we get $$(ax-a-x)(ax-x+1)(x-1+a)(-x+a)(ax-1)(ax-a+1)=0$$

Answer 3

$$\frac{(x^2-x+1)^3}{x^2(x-1)^2}=\frac{(a^2-a+1)^3}{a^2(a-1)^2}$$

Now multiply both sides by $x^2(x-1)^2$ :

$$(x^2-x+1)^3=x^2(x-1)^2\frac{(a^2-a+1)^3}{a^2(a-1)^2} \\ \implies (x^2-x+1)^3-x^2(x-1)^2\frac{(a^2-a+1)^3}{a^2(a-1)^2}=0$$

Without expanding, it can be written as :

$$x^6+a_1x^5+a_2x^4+a_3x^3+a_4x^2+a_5x+1=0$$

Since, product of roots of this equation is $1$, each solution's reciprocal will also be a solution to this equation.

Answer 4

Hint:  write the LHS in terms of $z = x+\cfrac{1}{x}$ as follows:

$$ \require{cancel} \frac{(x^2-x+1)^3}{x^2(x-1)^2} = \frac{(x^2-x+1)^3}{x^2(x^2-2x+1)}= \frac{\bcancel{x^3}\left(x+\cfrac{1}{x}-1\right)^3}{\bcancel{x^3}\left(x+\cfrac{1}{x}-2\right)}=\frac{(z-1)^3}{z-2} $$

Let $b=a+\cfrac{1}{a}$ and do the same for the RHS, then the equation becomes:

$$ \frac{(z-1)^3}{z-2} = \frac{(b-1)^3}{b-2} $$

The above is a cubic in $z\,$ with the obvious root $z_1=b\,$, which leaves a quadratic to solve.

$$ \big(\,z-b\,\big) \,\big( \,(b-2)z^2 +(b-2)(b-3)z - (2b^2-6b+5)\,\big) \,=\, 0 $$

After not too pretty calculations, the other roots turn out to be:

$$ z_{2,3} = \frac{b^2 \pm (\sqrt{b^2 - 4} - 5) b \mp \sqrt{b^2 - 4} + 6}{4 - 2 b} $$

Reverting to the $x$ and $a$ variables, the root $z_1=b$ gives the roots $x=a$ and $x=\cfrac{1}{a}\,$, then the roots $z_{2,3}$ give the other $4$ roots in $x$ after solving the respective equations. The calculations are again not pretty (and not included here), though noting $\sqrt{b^2-4}=a-\cfrac{1}{a}\,$ eliminates the radicals upfront.

---

[ EDIT ]  The following is a shortcut for the final calculations, using OP's observation that:

I see that if $x=x_1$ is a solution, then $x=1-x_1$ is also a solution.

This means that the second root in $z$ is $z_2=1-a + \cfrac{1}{1-a}\,$ corresponding to the roots $x=1-a$, $x=\cfrac{1}{1-a}\,$. The remaining root in $z$ as determined by Vieta's relations is:

$$\require{cancel}z_3=-(b-3)-\left(1-a + \cfrac{1}{1-a}\right)= -\bcancel{a}-\frac{1}{a}+3-1+\bcancel{a}-\frac{1}{1-a}=2 - \frac{1}{a}-\frac{1}{1-a}$$

Solving the equation $x+\cfrac{1}{x}=2 - \cfrac{1}{a}-\cfrac{1}{1-a}$ gives the last two roots $x=\cfrac{a}{a-1}\,$, $x=\cfrac{a-1}{a}$.

---

[ EDIT #2 ]  Even shorter: once established that if $x$ is a root then $1/x$ and $1-x$ are also roots, and given the obvious $x=a$ root, it follows that $\,1/a\,$, $\,1-a\,$, $\,1/(1-a)\,$, $\,1-1/a=(a-1)/a\,$, $\,1/(1-1/a)=a/(a-1)\,$ are also roots. For $a \ne 0,1$ and $a \not \in \{-1, \frac{1}{2},2\}$ the $6$ roots are distinct, and since the equation is of degree $\,6\,$, it follows that these are the only roots. For $a \in \{-1, \frac{1}{2},2\}$ the same can be shown to hold true by a continuity argument.