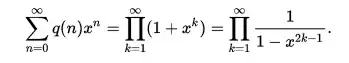Number of partitions for N without repetition

Question

I'm trying to figure out a formula that returns the number of strict partitions (no duplicate values) of n.

For example:

5 would yield 3: 5, 4+1, 3+2

I only need the number of unique partitions, not the partitions themselves.

I did come across this article: http://oeis.org/A000009 that has a reference to a table of outputs: http://oeis.org/A000009/b000009.txt that has exactly what I need, however I do not understand the referenced generating formula which is:

prod(m>=1, 1+x^m)

From that it appears that if my input is 5, I would never receive 3 as a result since that value is increasing exponentially.

I also found this reference http://mathworld.wolfram.com/PartitionFunctionQ.html which, as shown in figure 19, uses a partition function and a binomial coefficient but I don't want to set a specific value for the distinct parts.

I hope I explained this well and I apologize for any ignorance when it comes to these formulas, it's been a while since I've dealt with anything like this so some clarification would be much appreciated!

score 1 · Accepted Answer · edited Apr 13 '17 at 12:19

1

The table at OEIS says that $q(5)=3$, as you have computed. So everything is fine. The generating function is not the function $q(n)$ itself.

So there is no easy "explicit formula" for $q(n)$, but one can coompute it using the generating function, see here.

edited Apr 13 '17 at 12:19

Community

1

answered Mar 28 '17 at 15:21

Dietrich Burde

140,055

Ah, that makes sense. So I guess what I'm looking for is the actual function q(n). Would you happen to know what that is? All of the functions I'm seeing are generating functions. – Ryan Sayles Mar 28 '17 at 15:29
$q(n)$ is the number of strict partitions of $n$ and has the above generating function. So you have everything! – Dietrich Burde Mar 28 '17 at 15:33
Ok that makes perfect sense now. Thank you! – Ryan Sayles Mar 28 '17 at 16:33

Number of partitions for N without repetition

1 Answers1