The intuition for why maps correspond to planar graphs is that you can use a map to draw a planar representation of its graph.
(The comments are right that we need to be somewhat careful about what maps are, what kind of lines we are allowed to draw, and the difference between a graph a drawing of a graph. So to turn this intuition into a proof, we'll need to do some work once we figure out what the right definitions are.)
Start with a map (source):
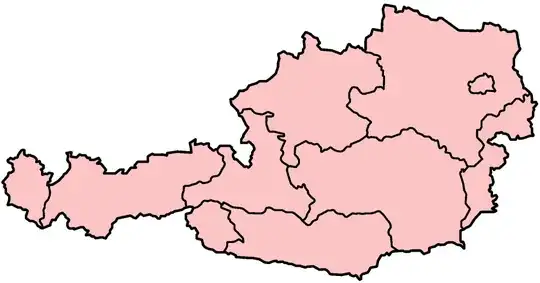
Its graph has a vertex for every region of this map, and an edge between two vertices if and only if the two corresponding regions are adjacent. The graph must exist; we must prove that it is planar. To do this, we will construct a planar embedding of this graph.
We begin by
- putting a vertex in each region, and
- whenever two regions border each other, putting a tick mark somewhere along the border.
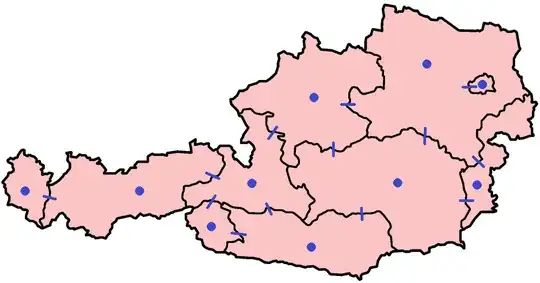
(Mathematically, the vertices and the tick marks are just points chosen either from the regions or from their borders.)
Now, within each region, draw paths from the vertex to the tick marks around each border:
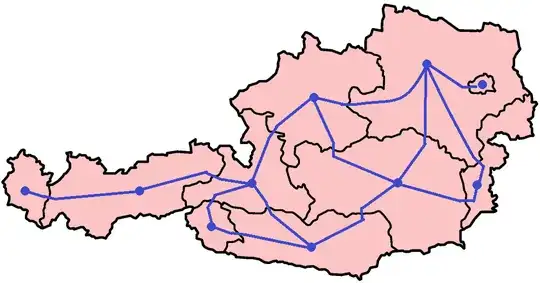
Care must be taken at this step that the paths we draw stay in the region they're at, and don't intersect each other. It's here that we need to think very carefully about our definition of what sort of regions a map is allowed to have.
The point of adding the tick marks, however, is that this step doesn't care at all about what the map looks like globally. All you have to do is to look at the regions one at a time, and draw paths from the vertex to the tick marks. We'll never have to worry about paths in one region intersecting paths in another, because all the paths we draw stay in a single region.
(You have to prove that you can avoid two paths in the same region intersecting each other. There's a number of ways to say "if there's an intersection point, we can deform the paths until there isn't", but this step is topology, not graph theory.)
At this point, you're done! We've constructed a planar embedding of the graph for our map in which no edges cross.


