1

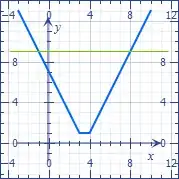
Is the method I used an efficient way of getting the answers to my titled question? From... $$\vert x-3 \vert + \vert x-4 \vert = 9$$ The way I solved this was to assume that each abs value was positive first giving: $$x-3 + x- 4 = 9 $$ $$2x- 7 = 9$$ $$x = -1$$ Then assuming they are both negative: $$-(x-3) + -(x-4) = 9$$ $$-x+3-x+4= 9$$ $$-2x+7= 9$$ $$x = 8$$

Solutions: $x = -1$ and $x= 8$

Alexander John
  • 562

4 Answers4

4

We have that

$$|x-3|+|x-4|=\begin{cases}-2x+7&\text{ if }x<3\\1&\text{ if }3\le x\le 4\\2x-7&\text{ if }x>4\end{cases}$$

So clearly $|x-3|+|x-4|=9$ implies that $x<3$ or $x>4$.

For $x<3$ we have $-2x+7=9$. The soultion is $x=-1$.

For $x>4$ we have $2x-7=9$. The solution in this case is $x=8$.

ajotatxe
  • 66,849
2

Take three intervals $$-\infty<x<3$$ $$3\leq x < 4$$ $$4\leq x<\infty$$ Then for first interval $$-(x-3)-(x-4)=9$$ $$2x-7=-9 \Longleftrightarrow x=-1$$

For second interval $$(x-3)-x+4=9$$ $$1=9$$ which is absurd

Finally for last interval $$2x-7=9\Longleftrightarrow x=8$$

NOTE:Your answers are wrong..You are not preserving equality when adding or subtracting numbers from your equations.

LM2357
  • 4,203
1

User35508 has given you the general algebraic method. But if you want some geometric intuition, your equation just says

$$\text{the distance from $x$ to $3$ plus the distance from $x$ to $4$ is $9$}$$

where distances are measured along the real number line.

This immediately explains why there are no solutions when $x$ is between $3$ and $4$. And with just a little more thought you can easily see the two solutions are $-1$ and $8$.

Of course, this geometric approach isn't very helpful for more complicated equations, e.g. $|x^2-5x+6|+|x-4|=3$, but it's a useful tool to have in your repertoire nonetheless.

symplectomorphic
  • 19,077
  • Yes, this is something I just discovered in another post. It is helpful to have that thought process behind these simple problems. I did kind of ignore it because of the fact that if the problems got more complex it would be difficult to imagine. Thanks. @symplectomorphic – Alexander John Mar 22 '17 at 14:49
  • The general algebraic strategy is casework: you must break your analysis of the equation into cases depending on where the expressions inside the absolute value bars change sign. In your problem, there are sign changes at $3$ and $4$, so you have three cases (though one is degenerate, i.e. leads to no solutions). In the more advanced example in my answer, there are sign changes at 2, 3, and 4, so you'd have four cases (some possibly degenerate). – symplectomorphic Mar 22 '17 at 14:53
0

This function is continuous and piecewise linear, with the pieces delimited by the values that cancel the arguments of the absolute value.

You can write this table of variations:

$$\begin{matrix}-\infty&3&4&\infty\\\hline\infty&1&1&\infty,\end{matrix}$$ which shows two solutions, in $(-\infty,3)$ and $(4,\infty)$.

enter image description here

These are obtained by replacing the absolute values by the appropriate signs,

$$-(x-3)-(x-4)=9$$ and $$+(x-3)+(x-4)=9.$$