Prove that we can construct a line segment with the length $\sqrt{n}$.

Question

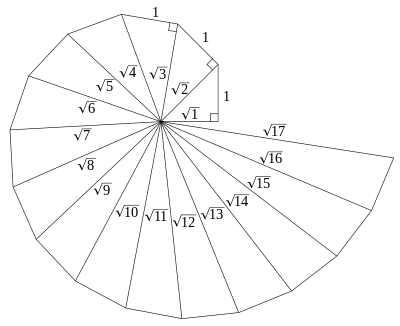
Question

If a line segment with the length $1$ is given then prove that we can construct a line segment with the length $\sqrt{n}$ for any $n \in \Bbb N$.

My approach:

I am looking for a solution using induction. For the base case it is obvious and like always the problem is the case $n+1$. I'm trying to use

$$n=(\sqrt{n+1}-1)(\sqrt{n+1}+1)$$

but I can't go further.

Any idea?

There's a typical way to construct $\sqrt{n}$. It's technically possible to do it with the rationals, too. I assume you don't want this? — Kaynex, Mar 13 '17 at 13:57

hmakholm left over Monica · Accepted Answer · 2017-03-13T13:59:43.463

5

Hint: If you have line segments of length $1$ and $\sqrt n$, then constructing a certain right triangle will give you something of length $\sqrt{1+n}$.

The classical solution -- without induction! -- is to construct $\sqrt n$ as the mean proportional between line segments of length $1$ and $n$.

edited Mar 13 '17 at 13:59

answered Mar 13 '17 at 13:55

hmakholm left over Monica

291,611

Oh, right! Thanks! – Arnaldo Mar 13 '17 at 13:56
We are not given length $n$, how can we use it in the second method? – N.S.JOHN Mar 13 '17 at 16:14
@N.S.JOHN: Supposedly you know the number $n$, so just put that many unit line segments after one another (e.g. extend the unit line segment you have indefintely and use the compass $n$ times to put equidistant marks on it). – hmakholm left over Monica Mar 13 '17 at 17:07

score 3 · Answer 2 · answered Mar 13 '17 at 15:28

3

You are perhaps looking for something like the Spiral of Theodorus, an incremental set of right triangles with the root of every integer as the hypotenuses.

Picture from Wikipedia:

answered Mar 13 '17 at 15:28

Joffan

40,356

Prove that we can construct a line segment with the length $\sqrt{n}$.

2 Answers2