Why do we differentiate?

Question

I'm currently learning how to differentiate, but as most entirely new things are rather abstract, I cannot really get a hold of the reason why I'm differentiating.

For example, we have a function, $y=x^3$. The derivative of $x^3$ is written as $y'=3x^2$. The differential of $x^3$ could be written as $d(x^3)=3x^2\,dx.$

Okay, I think. What then, I wonder? This is not really telling me anything. Beautiful math, though.

(The answers to what is the use of derivatives do not give me very much mathematical intuition behind why we differentiate.)

Answer 1

This is not really telling me anything.

It is telling you something very important.

The derivative of a function $y = f(x)$ at $x$ is defined as $$f'(x) = \lim_{h\to 0}\dfrac{f(x + h) - f(x)}{(x+h) - x}$$ Now, try to analyse the expression. What do we mean by $f(x + h) - f(x)$? That is nothing but the change in $y$. And what do we mean by $(x + h) - x$ ? It is the corresponding change in $x$ which evaluates to $h$.

In the image, $f(x+h)-f(x) = AC$ and $h = BC$. $$\dfrac{f(x + h) - f(x)}{h} = \dfrac{AC}{BC}$$ And $\dfrac{AC}{BC}$ is the slope of the secant $AB$. Now, if $h$ gets closer and closer to $0$, the point $A$ will get closer and closer to point $B$, given the function is differentiable (which also implies it is continuous). In the limit as $h$ approaches $0$, $A$ would come infinitesimally close to $B$.

Therefore, the expression $$\lim_{h\to 0}\dfrac{f(x + h) - f(x)}{h}$$ would give us the slope of the tangent line to the graph at point $B$. This is what the derivative tells us. It gives the slope of a function at a given point.

Why do we differentiate?

Because derivative gives you the rate of change of $y$ with respect to $x$. And this information is used widely in physics. For example if you are given the displacement an object as a function of time and you want to know its velocity at a particular point of time, you need to find the derivative of the displacement function with respect to time to get velocity as a function of time (because velocity is the rate of change of displacement with respect to time).

Answer 2

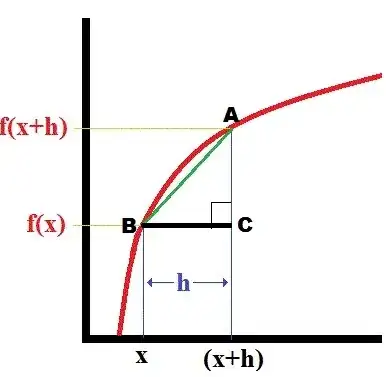
Differentiating gives the rate of change of a function. It is used any time you want to study how the change of one variable affects another. It has many practical examples.

Physics:

One, a physics example, being that the velocity is the derivative of the position function.

$$ s(t) = s_0 + v_0 t - \frac{1}{2}gt^2 \quad\text{# Position of an object at time }t$$

$$ v(t) = s'(t) = -gt + v_0 \quad\text{# Velocity of an object at time } t$$

$$ a(t) = v'(t) = -g \quad\text{# Acceleration of an object} $$

Note: Here $g$ is the acceleration due to gravity ($-9.8 \frac{m}{s^2}$), $v_0$ is the initial velocity, and $s_0$ is the initial position.

Analysis:

The derivative can also be used for many other branches in mathematics. The branch mathematical analysis deals with analytic functions, rate of change, and therefore derivatives. For instance, one can approximate a function using a sum up to the n-th derivative in a Taylor Series

$$ f(x) = \sum_{n=0}^{\infty} \frac{(x-\alpha)^n}{n!}f^{(n)}(\alpha) $$

The derivative can be used to find information about a function such as maximums and minimums. All relative maxes and mins of $f(x)$ will lie on a point where $f'(x)=0 \text{ or is undefined}$. These are called critical points. In addition where $f''(x)=0 \text{ or is undefined}$ and changes signs represents a change in concavity of $f$.

Answer 3

Consider a very basic formula that relates velocity, position, and time: $v = \frac{\Delta x}{\Delta t}$. Notice that velocity is the rate at which position changes over time. However, the formula given only works if the velocity is constant, i.e., if our position consistently changes the same amount for each unit of time. Otherwise, if we use this formula when the velocity is non-constant (say a car drive through a crowded city), then this formula will only give us an average velocity.

However, differentiation allows us to calculate rates of change even when those rates of change are not constant. So instead of calculating $v = \frac{\Delta x}{\Delta t}$, we instead calculate $v = \frac{dx}{dt}$ which will tell us the instantaneous velocity at any point $x$. You can almost think of the derivative as a "fancy division" between two changing quantities.

Answer 4

When you differentiate, you a finding a function for the slope of the tangent to a curve at any given value of $x$.

For example, if you differentiate $y=x^2$, the function for the slope will be $\frac{dy}{dx}=2x$. Therefore, at $x=1$, the slope of the tangent will be $m=2$ as shown below:

This is also important in problems such as finding local minimum and maximum values of a function, especially in optimization problems. Therefore, this is especially useful in engineering. For example, to find the minimum of $y=x^2$, we can differentiate and set $\frac{dy}{dx}=0$. This tells us that the minimum value of $y$ is at $x=0$, which has coordinates $(0,0)$.

Answer 5

Derivatives (and calculus) were born to solve physics' problems. Derivative represents how one quantity changes as another quantity varies. In many cases, we can construct models by relating quantities to their rates of change, then using tools from differential equations to make predictions. That's why we study derivatives!

Answer 6

Differentiation simply means finding out the derivative, or the slope of the tangent line at any point on the graph of the function. Finding derivatives is just finding out the instantaneous rate of change of a function, and since it is instantaneous, it is calculated at a particular x value, if the function is defined as $$y=f(x)$$

It is easy to find out the slope of a line between any 2 points, if we know the coordinates of the points, but to find out the slope when only one point is known, the derivative comes into play. If you have a curve and are asked to find out the rate of change or at what rate does the value of the function change with respect to the variable at one particular point, you can use the first principle which you must be knowing, or other differentiation rules accordingly.

As you have shown, when you get $$y'= 3x^2$$, plug in various $x$ values to know what the slope of the tangent line is at that $x$ value.

So, in a nutshell, we differentiate (or find out the derivative) in order to find out the instantaneous rate of change of the function with respect to the variable.