1

I approached it by drawing the right triangle, and then drawing $c^2$ as a square. I then split the square into fourths, and showed that the right triangle was a fourth of $c^2$. Is this how I approach the question?

Gerard L.
  • 2,591

4 Answers4

2

A pure Euclidean Geometry approach:

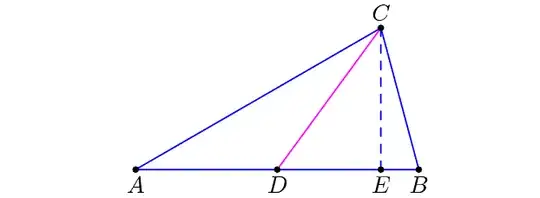
Triangle

Name the triangle $ABC$ with $AB$ the hypotenuse. Let $D$ be the midpoint of $AB$ and $E$ the foot of altitude $CE$.

Now it's well known that $CD=\frac{1}{2}AB.$ Also $CE\le CD$ since $CE$ is the shortest distance from $C$ to $AB.$ So $$\text{Area of }\triangle ABC=\frac12\cdot AB\cdot CE\le \frac12\cdot AB\cdot CD=\frac12\cdot AB\frac12 AB=\frac14\cdot AB^2=\frac14c^2.$$

That's what we had to prove. $\blacksquare$

Community
  • 1
Ankoganit
  • 740
1

Four replica of the triangular are less than the square Geometrically, four replica of the triangle are less than the square. This suggest the following proof:

Denoting $a$ and $b$ (with $a\le b$) the sides of the triangle. The side of the inner square is $b-a$, then the total area of the large square is $$(b-a)^2+4\times\frac{ab}{2}=a^2+b^2$$ which is an obvious identity. Then, with $a^2+b^2=c^2$, $$\frac{ab}{2}=\frac{1}{4}\left[c^2-(b-a)^2\right]\le \frac{c^2}{4}$$

Community
  • 1
Paul Enta
  • 15,313
0

Using Sine Law, $$\dfrac a{\sin A}=\dfrac b{\sin B}=\dfrac c{\sin90^\circ}$$

$\implies a=c\sin A$ and $b=c\sin B=c\sin(90^\circ-A)=c\cos A$

So, the area $$\dfrac12(c\sin A)(c\cos A)=\dfrac{c^2\sin2A}4$$

lab bhattacharjee
  • 279,016
0

$$c^2=a^2+b^2$$

Now area $=\dfrac12ab\sin90^\circ$

Again $(a-b)^2\ge0\iff2ab\le a^2+b^2=c^2$

lab bhattacharjee
  • 279,016