An interesting question! And the answer is, yes, it is possible. Also, I'm pretty sure my solution is the shortest path possible (i.e. I can't think of a shorter way to do it).
Some initial definitions and constants: The cottage is located at $(0,0)$, the excavator is initially located at $(8,0)$, the starting radius of the fire is $r_s = 5$ m, the minimum distance the excavator must keep to the fire is $d_{min} = 3$ m, the radial speed of the fire is $V_f=1$ m/h and the speed of the excavator is $V_e=8$ m/h.
Now, the radius of the fire from the cottage at time $t$ will therefore be $$r_f(t)=r_s+V_f * t$$
The radius the excavator must maintain to the cottage at any time $t$ will thus be $$R(t)=r_f(t) + d_{min} = r_s+d_{min}+V_f * t \tag{1}$$
We now want to find the angle $\theta$ of the excavator. But let us first look at how the excavator should move in a small time interval $dt$:
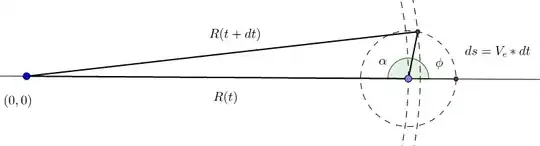
As shown above, the excavator should move at full speed in a straight line so that it is exactly at the new minimum distance from the fire at time $t+dt$. The angle $\alpha$ at which it needs to move can be found using the Cosine rule: $$cos(\alpha) = \frac{R(t)^2+(V_e \, dt)^2-R(t+dt)^2}{2R(t)V_e \, dt}$$
Inserting the formula for $R(t)$ and letting $dt \to 0$ we find that $$\lim_{dt \to 0} cos(\alpha) = -\frac{V_f}{V_e}$$
We see that the angle $\alpha$ is a constant. This rings a bell. We remember that the logarithmic spiral has a constant angle, call it $\phi$, between the tangent to a point and the radial line to that point. The angle $\phi$ is indicated in the figure above and we see that $\phi = \pi - \alpha$. So if $\alpha$ is a constant, then $\phi$ must be a constant and it therefore seems we are dealing with a logarithmic spiral. Let us assume this is the case and see what happens.
A logarithmic spiral is defined by the equation $$R=a \, e^{b \theta}$$
We now need to find $a$ and $b$. From the previous link we know that $tan(\phi) = \frac{1}{b}$, which means $tan(\pi-\phi) = tan(\alpha) = -\frac{1}{b}$. We can express $tan(\alpha)$ in terms of $cos(\alpha)$ in the following way: $$tan(\alpha) = \frac{\sqrt{1-cos(\alpha)^2}}{cos(\alpha)}$$
which means $$b= \frac{V_f}{\sqrt{V_e^2-V_f^2}}$$
We now know $b$. To find $a$ we use the boundary condition that at $\theta = 0$ we must have $R= r_s+ d_{min}$. This gives $a=r_s+ d_{min}$ and we have the following equation for the movement of the excavator: $$R=(r_s+ d_{min}) \, e^{\frac{V_f}{\sqrt{V_e^2-V_f^2}}\theta}\tag{2}$$
Inserting the values of the constants into equations $2$, we can plot the path:
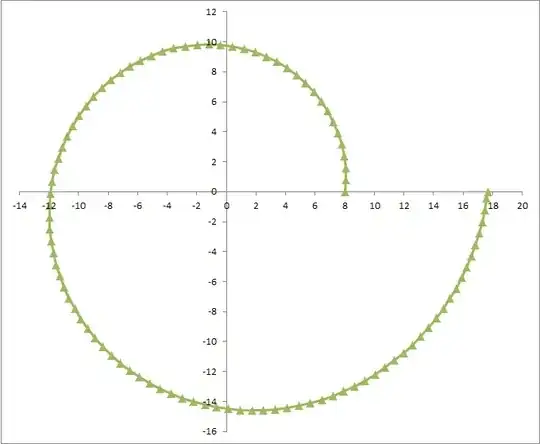
As expected we get a spiral. Each marker on the spiral is the excavator's position at intervals of $0.1$ hour. We can check that at any time $t$ the excavator is at the minimum distance required, $R(t)$. We can also check that the straight line distance covered by the excavator, between one marker and the next ($0.799565$ at the second marker), is almost, but not quite, $V_e \, dt$, which is as expected when we know that the actual path between one marker and the next is not a straight line, but a curve. Our assumption that the curve is a logarithmic spiral seems vindicated.
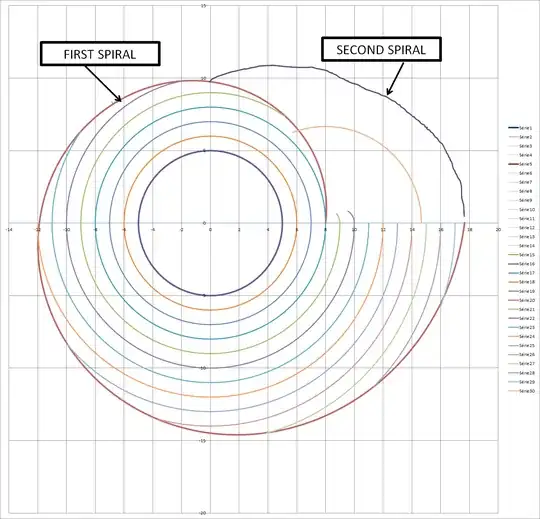
Anyway, on with the problem. The spiral completes its first loop when $\theta(t) = 2\pi$. Using equation $2$ we can calculate that this occurs at $R(t) \approx 17.6555$ meters and using equation $1$ we find this occurs at $t \approx 9.6555$ hours. We know the fire reached the excavator's starting point after $3$ hours. That point then became a new center of fire, spreading outward and upward at its fixed speed. When the excavator completes the first loop, the fire has thus been spreading from this point for $t=9.6555-3 = 6.6555$ hours, and will have a starting radius from this point of $r_{s2} = 6.6555$ meters. We thus have a situation equivalent to the original starting situation, just with a shifted center of fire, $x=8$ instead of $x=0$, a different starting radius of fire, $r_{s2}$ instead of $r_s$, and a different starting position of the excavator, $x = 17.6555$ instead of $x=8$. Using our equations (with these modifications) we can plot the last loop:

The second loop intersects the first loop at $(x,y) \approx (-0.3462, 9.7881)$ where the radius of the second loop is $\approx 12.8634$. The arc length of a logarithmic spiral is given by $$s = \frac{\sqrt{1+b^2}}{b}(r_2 - r_1)$$ where $r_1$ and $r_2$ are the starting radius and the ending radius of the arc. The total length of the excavator's path is therefore $$L = \frac{V_e}{V_f}[(17.6555-8)+(12.8634-9.6555)]$$
or
$$L \approx 102.9072$$