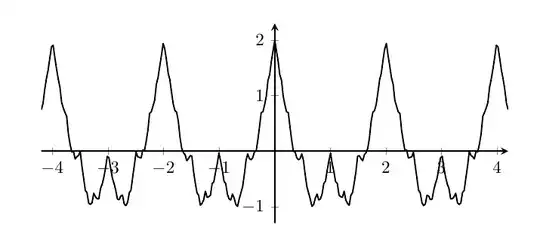
Is there a formal definition for the concept of nowhere differentiable function in $\mathbb{R}$?
I know that a function can fail to be differentiable in several ways in an open interval but I am looking for references. I am also familiar with the most common examples.