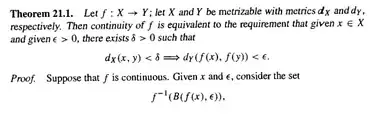3

Prove that the $\epsilon-\delta$ definition is equivalent to the topological definition of continuity

Below is a proof from Munkres' Topology A First Course

enter image description here

enter image description here

I understand everything in the proof except for the final argument. I don't understand how $x \in B_{(X, d_x)}(x, \delta) \subset f^{-1}(V)$ implies that $f^{-1}(V)$ is open.

For example a closed set could contain an open set, but that doesn't mean that the closed set is open.

Take $[0, 1] \subset \mathbb{R}$, $(\mathbb{R}, d)$ is certainly a metric space with the standard euclidean metric $d$, and the open ball centered at $\frac{1}{2}$ with radius $\frac{1}{3}$ is contained in $[0, 1]$ but $[0, 1]$ is not open, i.e. $B_{(\mathbb{R}, d)}(\frac{1}{2}, \frac{1}{3}) \subset [0, 1]$, but $[0, 1]$ is not open.

So my question is how is the final argument valid?

Anubhav Mukherjee
  • 6,708
Perturbative
  • 13,656

2 Answers2

2

The argument shows that $x$ is an interior point of $f^{-1}(V)$.

If this were true only for that one point $x$, then of course the argument would be wrong. But the argument shows that it is true for every point $x \in f^{-1}(V)$, which is why $f^{-1}(V)$ is open.

user414998
  • 251
0

Recall the following equivalent definition of an an open set in a metric space:

Let $X$ be a matrix space. Let $U \subseteq X$ be a set. If for all $x \in U$, there exists some open neighborhood $x \in B_x \subset U$, then $U$ is open.

This has to be true for every $x \in U$. In particular, we already found a neighborhood of $x$ by the $\epsilon-\delta$ condition, namely $B(x,\delta)$ so that $x \in B(x,\delta) \subseteq f^{-1}(V)$, and so the preimage must be open.

In your example $[0,1]$ is not open, since the element $1 \in [0,1]$ has no such neighborhood, since $(1+\epsilon) \notin [0,1]$ for all $\epsilon>0$.

Andres Mejia
  • 21,467