Centroid of polygon

Question

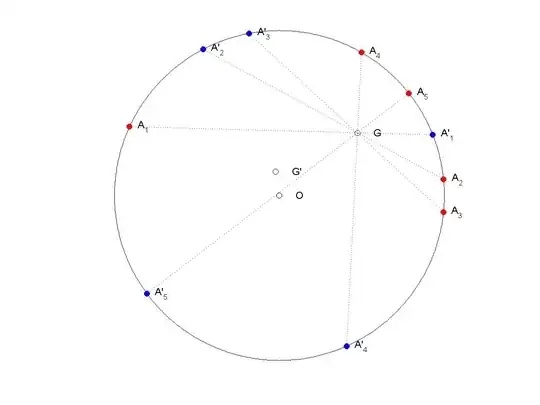
Let $A_1A_2...A_n$ be a polygon inscribed in a circle $\Gamma$ and $O$ its circumcenter. Let $A_k'=A_kG \cap \Gamma$, $k=\overline{1,n}$. If $G'$ is the centroid of $A_1'A_2'...A_n'$, prove that $OG' \leq OG$.

I tried using complex numbers, setting $O$ as the origin of the complex plan, but then I got stuck when I tried to calculate the modulus of $OG'$. Here's my approach:

WLOG let $|a_1|=|a_2|=...=|a_n|=1.$ It's obvious that $g=\frac{a_1+a_2+...+a_n}{n}$. Since $A_k, G$ and $A_k'$ are collinear, we know that $\frac{a_k-g}{g-a_k'} \in \mathbb{R_+}$ and this leads to $a_k'=\frac{g-a_k}{1-\overline{g}a_k}$. From now on, I don't know what to do with $|g'|=|\frac{\sum a_k'}{n}|.$

Answer 1

$a_k'=\cfrac{g-a_k}{1-\overline{g}a_k}$

You are almost done at this point. Write the above as:

$$a_k' - \bar g \,a_k \,a_k' = g-a_k \quad \iff \quad a_k' = \bar g \,a_k \,a_k' + g-a_k$$

Sum for all vertices:

$$ \require{cancel} \sum_{k=1}^n a_k' = \bar g \,\sum_{k=1}^n a_k\,a_k' + \bcancel{n\,g} - \bcancel{\sum_{k=1}^n a_k} \quad \iff \quad n\,g' = \bar g \,\sum_{k=1}^n a_k\,a_k' $$

Take the modulus, and use the triangle inequality:

$$ n\cdot|g'| = |g| \cdot\left|\sum_{k=1}^n a_k\,a_k'\right| \;\;\le\;\; |g|\cdot\sum_{k=1}^n |a_k\,a_k'| = |g|\cdot n $$

Therefore $\,|g'| \le |g|\,$.