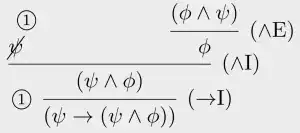How to solve this by natural deduction?

Question

I'm trying to solve this(Classical Propositional Logic) :

$$ \gamma \ \lor ( \lnot \ \gamma \ \lor (\ \psi \land \ \phi \ )) \, $$

I did this :

1. Assuming $$\psi,\phi$$
2. Introduction the $$\land$$ so $$(\ \psi \land \ \phi \ )$$
3. Now I can use the introduction of $$\lor$$ so $$\gamma \ \lor (\ \psi \land \ \phi \ )$$ 4).And now?

Sorry I my first post, and also I'm new in logical deduction, so please halp me and don't rate me wrong.
P.S I use Tree Proofs

Answer 1

Let $A = (\gamma \ \lor ( \lnot \ \gamma \ \lor (\ \psi \land \ \phi \ ))$. We want to prove $\vdash A$.

Assume $\neg A$ and $\gamma$.

From $\gamma$, by $\lor I$ we have $(\gamma \ \lor ( \lnot \ \gamma \ \lor (\ \psi \land \ \phi \ ))$, then by $\neg E$ we get $\bot$.

Now from $\bot$ using $\neg I$ we can discharge $\gamma$ and deduce $\neg \gamma$.

From $\neg \gamma$ using $\lor I$ we get $\lnot \ \gamma \ \lor (\ \psi \land \ \phi \ )$.

Using $\lor I$ again we can deduce $A$, and from $A$ and $\neg A$, using $\bot$ law, we get $\bot$.

From $\bot$, using $RAA$ we get $A$ and discharge $\neg A$, and the proof is complete.