Prove that the area of the region on plane bounded by $\max (|x|, |y|)\leq 1$ and $xy \leq \frac{1}{2}$ is $3+\ln(2)$
How to plot $\max (|x|, |y|)\leq 1$. Could someone help me with this?
Asked
Active
Viewed 1,828 times
1
-
In general, $\max(a,b)\le L$ if and only if $a\le L$ and $b\le L$. – Akiva Weinberger Jan 30 '17 at 15:20
-
Can you see that $max (|x|, |y|)\leq 1$ is the square centered in $0$ with sides of lenght $2$ – Tryss Jan 30 '17 at 15:28
-
Here's a graph - the blue is $\max(|x|,|y|)\le1$, and the red is $xy\le\frac12$. – Akiva Weinberger Jan 30 '17 at 15:39
-
@Tryss Could you elaborate how side would be 2 units? – user383014 Jan 30 '17 at 15:54
1 Answers
1
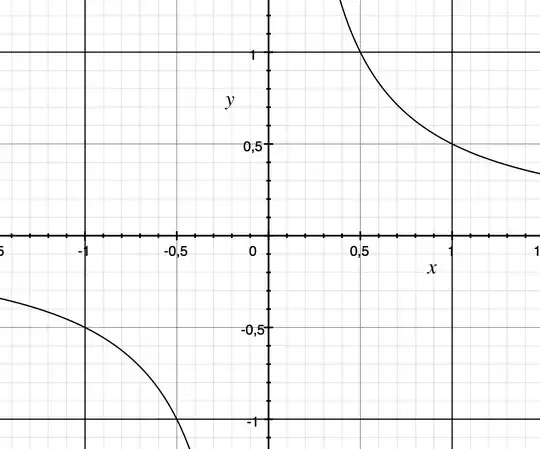
so we can do the integral to calculate the region between $$x\in\left(\frac{1}{2},1\right) \quad y\in\left(\frac{1}{2},\frac{1}{2x}\right)$$ that it is the same region between $$x\in\left(-1,-\frac{1}{2}\right)\quad y\in\left(\frac{1}{2x},-\frac{1}{2}\right)$$ and the last region have measure $3,5$ so: $$2\int_\frac{1}{2}^1 \int_\frac{1}{2}^{\frac{1}{2x}} dy\,dx=\int_\frac{1}{2}^1\frac{1}{x}-1\,dx= \Big[ \ln[x]-x\Big]_\frac{1}{2}^1=\ln[2]-\frac{1}{2}$$ so we have finish
Cuoredicervo
- 449