12

Today my daughter Ella asked me "Is a trapezoid an irregular polygon?" and I realized I cannot give her a definitive answer.

According to the Internet, trapezoids are alternately defined as having only one pair of parallel lines, and also at least one pair of parallel lines. My understanding is that this is simply an unresolved ambiguity in mathematics.

My question is, which definition has the stronger case? So far I have this:

The case for "only one":

  • Many people seem to think this is more intuitive and/or traditional

The case for "at least one":

  • Inclusive definitions are generally more useful (if this true I'd like to learn why)
  • It's the only definition that fits with the concept of trapezoidal sums in calculus

What am I missing?

Lee Whitney III
  • 253
  • 5
    You're not missing anything much. It's a mess (although only a naming-convention mess, not a mathematical difficulty). I'll note that technically the only regular four sided polygon is the square. Depending on whether you go inclusive or not, squares could be a special case of a trapezoid, or not. – Joffan Jan 29 '17 at 20:46
  • 1
    If we have "only one pair" of parallel lines, we have a trapezoid which is not a parallelogram. If we have "at least one pair", we have a trapezoid which can be a parallelogram as well. – Peter Jan 29 '17 at 20:48
  • The trapezoids occuring in trapezoidal sums are in general no parallelograms and no rectangulars. So, the name "trapezoidal sum" makes perfectly sense – Peter Jan 29 '17 at 20:51
  • @Peter, I don't think this is correct. My understanding is that trapezoidal sums are for use with curves, and since all lines are curves, this would allow trivial cases where the "only one pair" definition would not make sense. – Lee Whitney III Jan 29 '17 at 21:48

3 Answers3

12

The idea of having "exclusive definitions" that put types of quadrilaterals into buckets instead of a hierarchy is a holdover from antiquity (even back to Euclid, if my vague memory of what I read is true.) I think its main proponents are often people who learned (and now teach) these mathematical ideas dogmatically, without a full appreciation of 20th century advancement in presentation of mathematics.

To add to the confusion, this paradigm is inconsistently applied, as the same people who use the exclusive-version definition of trapezoid do not usually also declare that rectangles are nonsquare.

In short, the inclusive-version definition of trapezoids (your second definition) definitely has a stronger case in terms of modern mathematics. I found in my searches that outside of American K-12 education (i.e., in higher education, and basically any non-American school) the inclusive version was the definition taken for granted. (That is not a definitive description: perhaps the problem does pervade other places.)

I did some research on this in the past, and found many good resources on the topic. I wrote a rather detailed answer with a bibliography at this link, and I think you will be interested in checking it out. The main book cited there will show you that there isn't really any virtue gained by using the exclusive-version, and that there are virtues for using the inclusive-version.

Community
  • 1
rschwieb
  • 160,592
  • Great answer esp. with the other background. Is the idea of inclusive definitions being generally more useful specific to geometry? In computer science we can't move without bumping into a hierarchy so I appreciate that aspect. However I don't see intuitively an inherent advantage outside geometry. Inclusive, exclusive, whatever, maybe I'm too biased by exposure to logic gates (https://en.wikipedia.org/wiki/Truth_function)? – Lee Whitney III Jan 29 '17 at 22:12
  • 2
    @Lee Oh, the inclusive version is almost universally better in all branches of mathematics. Suppose you prove a theorem for trapezoids. In all likelihood, the theorem is true for parallelograms too. If you're using the exclusive definition of trapezoid, you have to prove everything over again for parallelograms. The inclusive definition sidesteps that problem. (This is one of the virtues mentioned in the sources.) – rschwieb Jan 29 '17 at 22:54
  • 1
    @Lee But also be aware that some CS people don't make use of logical hierarchy. I base this assertion on two experiences: first I saw it claimed in documentation that a "deque generalizes a queue," but when I made a suggestion that this was backwards, I was flatly rejected. Secondly, I saw a work in which an author demonstrated inheritance of properties in quadrilaterals using object oriented programming, but a CS professional gave it a scathing review saying that it was nonsense (based on design.) So (cont'd) – rschwieb Jan 30 '17 at 01:03
  • 1
    @Lee (cont'd) I think that it is not first nature to many computer programmers. Later on I learned about the circle ellipse problem and decided perhaps that some programmers do not use the logical hierarchy model to think about things because it's not good with OOP – rschwieb Jan 30 '17 at 01:04
3

Short answer is that the definition being used should be explicitly spelled out in every context where it actually matters.

Inclusive definitions are generally more useful (if this true I'd like to learn why)

Take for example the area formula: if a quadrilateral has a pair of parallel sides, then its area is half the distance between the two parallels times the sum of those two sides.

The theorem obviously holds true for arbitrary trapezoids, but also for parallelograms, rhombi, rectangles and squares. If you defined each one in the strictest non-inclusive sense, then you would technically have to restate and/or prove the theorem separately for each shape in turn.

dxiv
  • 77,867
  • "Short answer is that the definition being used should be explicitly spelled out" Maybe so, but what rubs me wrong it that I don't believe it's good to propagate the thinking that ambiguity in math is acceptable. I don't see why there can't be consensus. – Lee Whitney III Jan 29 '17 at 22:17
  • 2
    @Lee There is no ambiguity as long as everything is clearly defined in the applicable context. Yes, it would be nice to have a consistent, universally accepted terminology, but reality is we don't. For a completely different example, the field of complex numbers includes the reals, of course. Yet, in some contexts, "complex" is used in the exclusive sense, in place of "non-real complex" e.g. "let $\omega$ be a complex $3^{rd}$ root of unity" with the meaning that $\omega^3=1$ but $\omega \ne 1$. – dxiv Jan 29 '17 at 22:40
  • 1
    @Lee: I fully agree with you, but I also fully agree with dxiv. If you ever attempt to write a textbook and ensure that every theorem is precise and correct, then you will quickly find that defining "trapezoid" to exclude parallelograms will make your geometry and real analysis life 'terrible', in the sense that you will quickly regret not having been more inclusive, since the inclusive definition translates to more elegant theorems and definitely less writing. =) – user21820 Jan 30 '17 at 09:16
  • 2
    @dxiv: I personally never use "complex" exclusively. It's not even useful in complex analysis, such as when you want a primitive 6th root of unity, and merely being imaginary isn't good enough. As you can see, I use the term "primitive", which is not only precise but also short. – user21820 Jan 30 '17 at 09:18
2

It's something of a truism to say that inclusive definitions are better, because any properties proved of a more general category automatically apply to all special cases contained within it.

However, consider the following theorems:

Theorem. The angle bisectors of any rectangle intersect at four points which form the vertices of a square.

Theorem. The perpendicular bisectors of any rhombus intersect at four points which form the vertices of another rhombus.

(See Figures.)

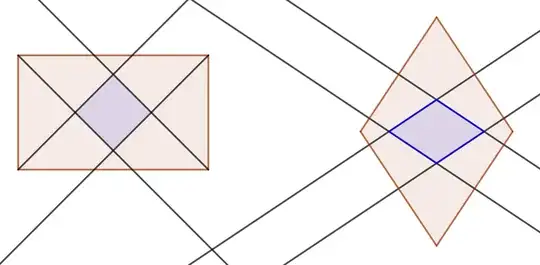
enter image description here

These theorems are true statements if rectangle and rhombus are defined exclusively, i.e. if "rectangle" is defined as "a quadrilateral that is equiangular but not equilateral" and if "rhombus" is defined as "a quadrilateral that is equilateral but not equiangular". However, if inclusive definitions are used, these theorems are false, because if the rectangle (resp. rhombus) is a square, then the angle bisectors (resp. perpendicular bisectors) would be concurrent, and the "figure" formed by them would be a single point.

In other words: the theorems are true for the general category only if the more specific category is excluded. Depending on whether or not you think these theorems are things you want to be true in your theory, this could be a reason in support of adopting exclusive definitions.

There is another option, of course: one could define "rectangle" and "rhombus" inclusively, but in the statement of the theorem specify in the hypothesis that it is true of a non-square rectangle or a non-square rhombus. But if you have to do this often enough, at a certain point it might make sense to introduce a name for "non-square rectangle" and "non-square rhombus" -- and then we are right back to exclusive definitions again.

What about trapezoids, the topic the OP specifically asks about? As discussed in this answer, if trapezoids are defined exclusively, then it is possible to calculate the area of a trapezoid given only its four lengths (provided you know which ones are the parallel ones and which ones are the non-parallel ones). (Even if you do not know which sides are the parallel ones, you can determine that the area must be one of six uniquely determined possible values.) However, if trapezoid are defined inclusively, then the four lengths do not determine the area at all, as the area of a trapezoid with side lengths $a,b,a,b$ can take on any real value between $0$ and $ab$.

(Related: For historical background on when the "inclusive" definitions of quadrilaterals came to be standard, see also this answer on MESE.)

mweiss
  • 24,547
  • "But if you have to do this often enough, at a certain point it might make sense to introduce a name for "non-square rectangle" and "non-square rhombus" -- and then we are right back to exclusive definitions again." Have we actually had to do this enough? Your example is one I've never used in class. If Pearson's Geometry never involves us in the distinctive properties of non-parallelogram trapezoids and non-rhombus kites, it still seems more convenient to allow all parallelograms to be trapezoids and all rhombi to be kites. – Chaim Mar 20 '18 at 11:47
  • @Chain Oh, agreed -- I actually think inclusive defs are better. I'm just pointing out that the common argument that properties are automatically inherited by special cases is not actually true. – mweiss Mar 20 '18 at 13:29
  • 2
    I guess that the fundamentalist who said that properties are automatically inherited by special cases could counter that in your counterexamples the point of intersection should be considered a special case of the square or rhombus called-for by the theorem you cite. But I think I see your point, that not all elegance lies on the same side of this choice. – Chaim Mar 20 '18 at 14:34
  • @Chain Yes, regarding the point of concurrency as a degenerate quadrilateral is one way out of the trap. But then when stating properties of squares you have to keep saying "non-degenerate" all the time. I think this is what Lakatos calls a choice between monster-barring and lemma-incorporation. – mweiss Mar 20 '18 at 14:37