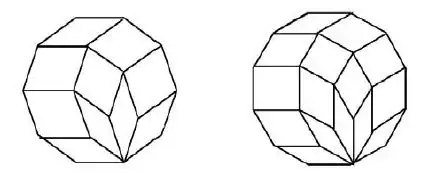
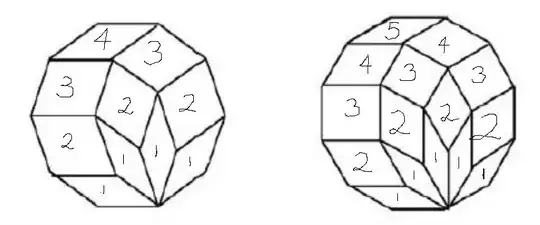
A regular decagon and a regular dodecagon have been tiled with rhombuses. In each case, the sides of the rhombuses are the same length as the sides of the regular polygon.
How many rhombuses will be there in a tiling by rhombuses of a $2002$-gon?
$A) 2002$
$B) 500 × 1001$
$C) 1000 × 1001$
$D) 1000 × 2002$
Could someone share please share the thought process of this question? I am not able to initiate it.