4

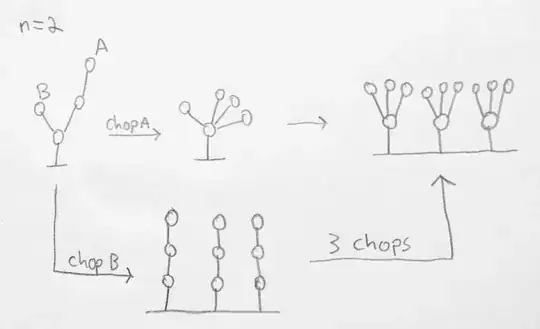
The Kirby-Paris hydra, previously seen on math.stack here and in this layperson-targeted video, is a one-player game that models the mythical hydra as a tree. Each node/vertex of the tree is considered to be a "head" of the hydra, except for the root which is its "body". A player "moves" by selecting a leaf node L and removing it. Then, the hydra "regrows" n copies what is left of L's parent's subtree, all rooted on L's grandparent. For our purposes, let n=2. The goal is to reduce the hydra to its body.

The surprising result is that, not only is the game winnable, it is impossible to lose. Any hydra will be "defeated" by a sufficiently long but finite sequence of moves. However, it seems that the sequence length grows very rapidly with increasingly complex hydra.

My question is whether the choice of moves has any effect on how many moves are required to defeat a particular hydra. If all sequences of moves have the same length, how is this proven? If there exist at least two sequences of different lengths, how may one find the shortest one?

Community
  • 1
mgold
  • 293
  • Note that there's an arbitrary choice being made; at every step of the process you choose an $n$ and replicate a subtree $n$ times. You can always choose $n=0$, in which case all sequences clearly have the same length (if there are $n$ nodes in the tree, then it always takes $n-1$ moves - can you prove this?). If you fix an $n\gt 0$, e.g. $n=2$ then I suspect moves don't 'commute' and thus order can matter, but I haven't really tried an example yet to prove it one way or the other. – Steven Stadnicki Jan 27 '17 at 01:17
  • It is preferable that the context necessary to understand the problem be included within the post, and not require external reference. – Math1000 Jan 27 '17 at 02:55
  • 1
    I have tried to briefly explain the problem and specified n=2. – mgold Jan 27 '17 at 04:06
  • 1
    This is a great question (and I +1ed a while ago). For that matter, is anything known about the slowest way to defeat the Hydra? Is it even known that the killtime isn't independent of how you play? – Noah Schweber Feb 05 '17 at 20:47

1 Answers1

2

First, a bit of terminology. Define k heads, growing out of one head, growing out of the body, as a k-fork. Define k heads growing out of each other in sequence, without any branching, as a k-chain.

As stated in the question, assume each chop produces n=2 copies, not counting the one already present.

Proof: Order can matter

Consider this diagram in which you start with a hydra on the top left (the horizontal line is the body/root). Chopping the higher head labeled A produces four-fork. There is no meaningful choice; the second chop yields three three-forks.

Suppose instead you chopped the lower head labeled B. This yields three three-chains. Chopping the top head of a three-chain yields a three-fork. Doing this for each chain gets us to three three-forks, but this takes four moves when before it took only two.

A diagram showing how a particular hydra may be reduced to another hydra along two paths of unequal length

Having gotten to the same hydra using a different number of moves, it follows that there are two complete sequences to kill this hydra that have different lengths. (Incidentally, three three-forks take 120 chops to kill, regardless of order.)

Conjecture: Kill the highest head

The shorter path in the example above was to kill the highest head, the one furthest from the body. I conjecture that this will always lead to defeating the hydra in the fewest number of chops. Conversely, I conjecture that the longest sequence is found by killing the leaf head closest to the body.

Imagine that the leaf labeled A in the diagram is replaced by a large subtree. Chopping B will then duplicate that subtree twice, creating a lot of heads. Chopping higher leafs causes the hydra to regrow smaller subtrees, adding fewer heads. Each head requires a chop to kill, so adding fewer heads is a good thing. The total number of chops equals the number of heads produced plus the initial number of heads.

However, I can't prove that greedily producing the fewest possible heads with each chop will result in a global minimum. It's possible that producing more heads now will allow one to produce fewer heads later.

mgold
  • 293