How can I find the parametrization of the curve given by the intersection of the sphere $x^2+y^2+z^2=81$ and the plane $x+y+z=15$.
Also it says that this intersection is a circle (clearly) with center $(5,5,5)$, and that $(7,4,4)$, $(4,7,4)$, $(4,4,7)$ are points on the curve (I don't know if this information is useful for the parametrization)
My try was to substitute $z$ in the sphere equation with the expression obtained for $z$ in the plane equation, but I can't conclude this way.
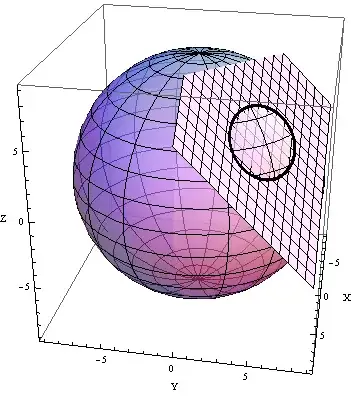
Method 1 (following your first step)
The projection in the $xy$ plane that you get is an ellipse, but it is not a horizontal nor a vertical one.
If the equation in $x$ and $y$ that you got was a quadratic form, then you could reduce it and find its canonical representation by standard procedures seen in linear algebra.
In this case we can use the same trick that was used in the answer here as follows.
Note that $$ 2x^2+2xy=2\left(x+\frac{y}{2}\right)^2-\frac{y^2}{2}\tag{1} $$ and let $X:=x+\frac{y}{2}$ and $Y:=y$, so that $x=X-\frac{Y}{2}$ and $y=Y$. Substituting in the equation you got (and making use of $(1)$), we obtain, after many simplifications, $$ \frac{(X-\frac{15}{2})^2}{(\sqrt{3})^2}+\frac{(Y-5)^2}{2^2}=1 $$ This is the ellipse in its canonical form and we have a standard parametrization for it (with $\theta\in[0,2\pi]$): $$ X(\theta)=\frac{15}{2}+\sqrt{3}\cos\theta\\ Y(\theta)=5+2\sin\theta $$ Hence, $$ x(\theta)=5+\sqrt{3}\cos\theta-\sin\theta\\ y(\theta)=5+2\sin\theta $$ and finally $$ z(\theta)=15-x(\theta)-y(\theta)=5-\sqrt{3}\cos\theta-\sin\theta $$
Here's a parametric plot of the parametrization.
Note: To be precise, the system $$ \begin{cases}x^2+y^2+z^2=81\\x+y+z=15\end{cases} $$ is equivalent to the system $$ \begin{cases}X:=x-y\\Y:=y\\\frac{(X-\frac{15}{2})^2}{(\sqrt{3})^2}+\frac{(Y-5)^2}{2^2}=1\\z=15-x-y\end{cases} $$ We need the equivalence in order to conclude that their solution sets are the same, that is, to conclude that our parametrization answers the initial problem.
Method 2
In $\mathbb{R}^3$, the parametrization $$ P(\theta):={\bf c}+r\cos(\theta){\bf u}+r\sin(\theta){\bf v},\quad\theta\in[0,2\pi] $$ where ${\bf u}$ and ${\bf v}$ are unit orthogonal vectors is one for the circle with center ${\bf c}$ and radius $r$ lying in the plane generated by ${\bf u}$ and ${\bf v}$ at ${\bf c}$.
With this in mind, the information that the intersection is a circle with center ${\bf c}:=(5,5,5)$ and that one of its point is ${\bf p}:=(7,4,4)$ is enough to find a parametrization.
First, $r=\|{\bf p}-{\bf c}\|_2=\sqrt{6}$.
Now, one can take ${\bf u}:=\frac{1}{\|{\bf p}-{\bf c}\|_2}({\bf p}-{\bf c})=\frac{1}{\sqrt{6}}(2,-1,-1)$.
Let ${\bf w}:=(w_1,w_2,15-w_1-w_2)$ and ${\bf v}:=\frac{1}{\|{\bf w}-{\bf c}\|_2}({\bf w}-{\bf c})$. Since ${\bf v}\perp{\bf u}$ if and only if $w_1=5$, we can take $w_2:=0$ for simplicity and we get ${\bf v}=\frac{1}{\sqrt{50}}(0,-5,5)$.
Here's a parametric plot of the parametrization.
Note: Of course, if you weren't given the extra piece of information, then you would have to check that the plane and the sphere do interesect. Also you would have to make sure that their intersection is not a single point, so that you could assume that it is a circle (which is geometrically clear?). This was noted in the comments by user @Leafar.
Since this is most likely a crafted exercise, you could have proceeded by inspection and tried integral values of $x$, $y$ and $z$ to discover that the point $(7,4,4)$ is in the intersection. Then from symmetry you would also see that $(4,7,4)$ and $(4,4,7)$ are in it.
To find the center of the circle, you could follow a vector normal to the plane from the center ${\bf o}$ of the sphere until it intersects the plane (as noticed by user @Doug M here): the point of intersection is the center ${\bf c}$. That this is plausible can be seen, perhaps, by translating the plane so that it becomes a tangent to the sphere at ${\bf t}$. Then the radius $\overline{{\bf ot}}$ is perpendicular to the plane and by symmetry (?) ${\bf c}$ has to lie on $\overline{{\bf ot}}$.
Here the center of the sphere is the origin, a vector normal to the plane is $(1,1,1)$ and $\alpha(1,1,1)$ is in the plane if and only if $3\alpha=15$, i.e. $\alpha=5$. Hence ${\bf c}=(5,5,5)$.
Final note: You can verify that if $P(\theta)=(x(\theta),y(\theta),z(\theta))$ then with both methods we have $$ x(\theta)^2+y(\theta)^2+z(\theta)^2=81\\ x(\theta)+y(\theta)+z(\theta)=15 $$ as it should be.
Also the arc lengths given by WolframAlpha in the links are nothing more than the circumference $2\pi\sqrt{6}$ of the circle.
I very much endorse the general method described in the answer from NeedForHelp (+1). Since I once worked out a scaled version of this problem (to produce material for my vector calculus class) let me share a trick solution to this specific problem.
The key features of the problem that my trick exploits are:
The third bullet tells us that $\vec{t}\perp (1,1,1)$ for all $t$. It also tells us that $2\vec{v}(t)$ has length $2\sqrt{3/2}=\sqrt6$. Furthermore, as $t$ varies, $2\vec{v}(t)$ over all the vectors with these properties.
So a parametrization for the curve of intersection is $$ \vec{r}(t)=(5,5,5)+2\vec{v}(t), $$ with $t$ ranging over the interval $[0,2\pi)$.
A Mathematica plot confirming this calculation:
In[1]:= pallo3 = ParametricPlot3D[
9 {Cos[u] Cos[v], Cos[u] Sin[v], Sin[u]}, {u, -Pi/2, Pi/2}, {v, 0,
2 Pi}, AxesLabel -> {"X", "Y", "Z"}, PlotStyle -> Opacity[0.7]]
In[2]:= taso3 = Plot3D[15 - x - y, {x, 0, 9}, {y, 0, 9}]
In[3]:= leikkaus3 =
ParametricPlot3D[
5 + 2 {Cos[t], Cos[t + 2 Pi/3], Cos[t - 2 Pi/3]}, {t, 0, 2 Pi},
PlotStyle -> Thickness[0.01]]
In[4]:= Show[{pallo3, taso3, leikkaus3}]
In addition to NeedForHelp's answer, if you want to emphasize the underlying symmetry of the problem, you may rewrite the parametrization as follows: $$\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\left(\begin{array}{c}5+2\cos\phi\\ 5+2\cos\Big(\phi+{2\pi\over3}\Big)\\ 5+2\cos\Big(\phi+{4\pi\over3}\Big)\end{array}\right)$$
