1

$z^4+i=0$ where $z \in \mathbb{C}$ should have $4$ roots by F $\theta$ C.

However I plugged this into Mathematica and it couldn't factorize it or find the roots. I tried myself, but by looking at the powers of $i$ I see:

$$i^2 = -1$$ $$i^3 = -i$$ $$i^4 = 1$$ $$i^5=i$$

that the fourth square root of $-i$ doesn't exists, as we are back where we started.

How do I factor this? And what are the roots?

Euler_Salter
  • 5,547
  • which site should I use? I am not asking about Mathematica.. I'm asking about maths – Euler_Salter Jan 19 '17 at 16:20
  • You should still use geometry rather than arithmetic. This is rather trivial in the complex plane using polar coordinates. – Arthur Jan 19 '17 at 16:20
  • 2
    Note that $-i=\cos \frac{3\pi}{2}+i\cdot\sin \frac{3\pi}{2}$ – math Jan 19 '17 at 16:21
  • Your statement that "the fourth root of -i doesn't exist" is not true. -u, like any complex number, has 4 fourth roots. While Math Chats "[tex]-i= cos\frac{3\pi}{2}+ i sin\frac{3\pi}{2}[/tex] is true, I would have written it as [tex]-i= i sin\frac{3\pi}{2}[/tex] s – user247327 Jan 19 '17 at 16:29
  • Compare with this question. – Dietrich Burde Jan 19 '17 at 16:33
  • 1
    Since you mention that Mathematica can't "factorize it or find the roots", you might be interested to know how you can help it along. You can find the roots using Solve. The format might look a bit strange but you can get it into format that you might expect (though, complicated) like so: FunctionExpand[ExpToTrig[z /. Solve[z^4 + I == 0, z]]]. Once you see that, you might try the Extension option of Factor: Factor[z^4 + I, Extension -> {Sqrt[2 + Sqrt[2]]}]. – Mark McClure Jan 19 '17 at 16:43
  • 1
    @MarkMcClure thank you a lot! – Euler_Salter Jan 19 '17 at 16:44
  • 1
    I've written the general solution to the equation $z^n = a$ with $a\in\mathbb C$ in this answer, if it helps. In your case it is $a = -i$. – Eff Jan 19 '17 at 16:52
  • 1
    Possible duplicate of What are the solutions to $z^4+1=0$? – Vladhagen Jan 20 '17 at 19:57

7 Answers7

5

Let us write the equation as $$z^4-a^4=0$$ for some $a$ to be determined.

We can factor as

$$(z^4-a^4)=(z^2-a^2)(z^2+a^2)$$ and with a little more effort,

$$(z-a)(z+a)(z-ia)(z+ia).$$

So the roots are of the form $a,ia,-a,-ia$, and we also have that $a^4=-i$. Without knowing how to extract the roots of a complex number, you can already write

$$(z-\sqrt[4]{-i})(z-i\sqrt[4]{-i})(z+\sqrt[4]{-i})(z+i\sqrt[4]{-i}).$$

To go further, you can use the polar form. Remember that the modulus of a product is the product of the moduli, and the argument of a product is the sum of the arguments.

Then the modulus of a fourth power is the fourth power of the modulus ($-i\to1$ in our case) and the argument of a fourth power is four times the argument ($-i\to3\pi/2$).

Hence, $$a=e^{i3\pi/8}.$$

You can also work this out directly, taking the square root twice.

$$(x+iy)^2=x^2-y^2+i2xy=-i$$

gives the system

$$x^2-y^2=0,\\2xy=-1.$$

Choosing $x=y$, we have the solution

$$\frac1{\sqrt2}(1-i).$$

Now let us solve

$$x^2-y^2=\frac1{\sqrt2},\\2xy=-\frac1{\sqrt2},$$ or after multiplication by $x^2$,

$$x^4-x^2y^2=\frac{x^2}{\sqrt2}$$ or

$$x^4-\frac{x^2}{\sqrt2}-\frac18=0.$$

One of the real solutions is

$$x=\frac12\sqrt{2+\sqrt2},$$ with $$y=-\frac1{\sqrt2\sqrt{2+\sqrt2}}=-\frac12\sqrt{2-\sqrt2}.$$

3

Hint: You need to find $$ z=\sqrt[4]{-i}=\sqrt[4]{e^{i(3\pi/2+2\pi k)}},\quad k\in\mathbf Z, $$ use the properties of the exponential function and see for which $k$ you'll get different roots.

Artem
  • 14,847
  • so in general when solving a complex polynomial, I should try to write it in exponential form based on the geometry? – Euler_Salter Jan 19 '17 at 16:30
  • Also, I've seen online that after the fifth order polynomial (I think) we cannot be sure we can factorise the polynomial, does it mean that we are always sure we can do it when the degree is less? – Euler_Salter Jan 19 '17 at 16:31
  • @Euler_Salter Yes, you should always use polar form of the complex numbers to find arbitrary roots. For the second question: you and mixing something. Any complex polynomial can be factorized in principle. What is different about 5th degree is that there exists no explicit formula to find roots. However, the roots always exist. – Artem Jan 19 '17 at 16:36
  • how can there not exist if we use exponentials? – Euler_Salter Jan 19 '17 at 16:37
  • 1
    @Euler_Salter there exists no general formula for an arbitrary polynomial. Your polynomial is not arbitrary ,and in your case you can easily find all $n$ roots to factorize $z^n+i=0$. – Artem Jan 19 '17 at 16:39
3

$$ \large \begin{align} z^4+i&=0\\ z^4&=-i\\ &=e^{i(2n-\frac 12)\pi}\\ z&=e^{i(\frac n2-\frac 18)\pi}\\ &=e^{-i\frac {\pi} 8},\; e^{i\frac {3\pi} 8},\; e^{i\frac {7\pi} 8}\; e^{i\frac {11\pi} 8} \end{align}$$

Hypergeometricx
  • 23,235
3

Write $-i=e^{3\pi i/2},e^{7\pi i/2},e^{11\pi i/2},e^{15\pi i/2}$ (i.e go around the circle in the complex plane a few times. Then take the $4^{th}$ root. Note that all angles should be less than $2\pi$

chrislutsko
  • 108
3

Multiply out $z^4$ when $z = \sqrt{\sqrt{2}-1}+\sqrt{\sqrt{2}+1}i$
$$ \left( \sqrt{\sqrt{2}-1}+\sqrt{\sqrt{2}+1}i \right)\left( \sqrt{\sqrt{2}-1}+\sqrt{\sqrt{2}+1}i \right) =\\ (\sqrt{2}-1) - (\sqrt{2}+1) +2 \sqrt{2-1}i = -2+2i \\ (-2+2i)(-2+2i) = 4 - 4 - 8i = -8i $$ So this $z$ gives something times $-i$, but it is too large by a factor of $\sqrt[4]8$. Thus one solution to $z^4=-i$ is $$ z =\frac{ \sqrt{\sqrt{2}-1}+\sqrt{\sqrt{2}+1}i}{\sqrt[4]8} $$ The other three solutions are, of course, this $z$ times $-1, i$ and $-i$, respectively.

How does one guess that original form? The best way I can think of is to use deMoivre's theorem, which leads to having to find the sine and cosine of $67.5^\circ$, which are the cosine and sine of $22.5^\circ$. You can then use the half-angle cosine formula on an angle of $45^\circ$, and that clues you into the presence of a square root of $\sqrt{2}/2 + 1$.

Mark Fischler
  • 42,297
2

Since $z^4=-i$, you're looking for the fourth roots of $-i$, which look like these points on the unit circle on an Argand diagram:

enter image description here

Note that complex $n$th roots of a number are always separated like this by $2\pi/n$ radians, so that when raised to the appropriate power they are "separated" by $2\pi \equiv$ coincident. Since $-i$ has an argument of $3\pi/2$, the "base" fourth root has an argument of $3\pi/8$.

Joffan
  • 40,356
  • so are they always evenly spaced by $2\pi / n$ ? – Euler_Salter Jan 19 '17 at 16:38
  • so now my question is.. since we know they are always evenly spaced by $2\pi / n$ is there an intuitive way, without using polar coordinates, to determine just one of them and hence go from there adding the angles? – Euler_Salter Jan 19 '17 at 16:44
  • Personally I would say that using polar coordinates is the intuitive way. $-i$ has an argument of $3\pi/2$ so the "base" fourth root has an argument of $3\pi/8$. – Joffan Jan 19 '17 at 16:45
2

We have $$ z^4 + i = 0 \iff \\ z^4 = -i \quad (*) $$ We now move to polar coordinates, expressing $z$ as $$ z = r e^{i\phi} $$ with radius $r \in [0, \infty)$ and angle $\phi \in [0, 2\pi)$. Then $(*)$ turns into $$ (r e^{i\phi})^4 = r^4 e^{4i \phi} = e^{i (3 \pi/2 + 2\pi k)} \quad (k \in \mathbb{Z}) $$ where we added the cyclic repetition of $e^{i\phi}$ to the right hand side.

Comparing both sides we have $$ r = 1 \\ 4\phi = \frac{3\pi}{2} + 2\pi k $$ which means $$ \phi = \frac{3\pi}{8} + \frac{k \pi}{2} = \frac{(3+4k)\pi}{8} $$ where $$ \frac{3\pi}{8}, \frac{7\pi}{8},\frac{11\pi}{8},\frac{15\pi}{8} $$ are in $[0, 2\pi) = [0, 16\pi/8)$.

This gives the roots $$ z \in \left\{ e^{3\pi i/8}, e^{7\pi i/8}, e^{11\pi i/8}, e^{15\pi i/8} \right\} $$

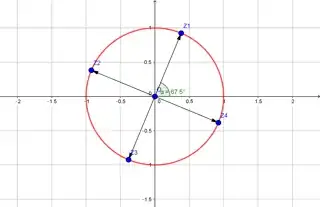
Unit circle with roots (Large version)

mvw
  • 35,114