Definition of convergence of sequences

Question

In my book, the definition is:

A sequence ${a_n}$, with $n = 0 \cdots \infty$, is convergent when there exists a number called $a$, which is a complex number, that satisfies that for every $\epsilon > 0$, there exists a natural number $N$ so that

$$|a_n - a| \leq \epsilon$$

when $n >= N$.

But it's like no matter how many times i read the definition, I don't understand it.

I know what a sequence is, I know what convergence mean, I know what complex numbers, natural numbers etc. mean and as I know, epsilon is just a variable like x and y for instance. But I don't understand the definition and it's driving me a bit insane why the authors of the book don't explain it in a way so that a person who are new to this kind of math can understand it.

Can someone explain the definition in a way so that it is easier to understand and why it is the way it is?

Answer 1

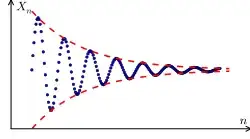
The important thing about a convergent sequence is that the convergent behavior has nothing to do with the first few terms; it doesn't have anything to do with the first hundred terms, or the first billion terms, or any given number of terms. The convergence is a property of the "tail".

The math is just saying (in technical language) what you intuitively know: that by going far enough out into the tail of the sequence, you can guarantee that EVERY TERM IN THE TAIL FROM THAT POINT ON is as close to the limit as you want.

How far do you need to go? Well, it depends on how close to the limit you want the tail to be. In fact, YOU don't get to choose that -- I get to say how close ("within $0.000001$") and then you have to go out into the tail and find a point where the entire rest of the tail is within MY SPECIFIED CLOSENESS of the limit. In a specific example, maybe you found that if you go out to the $537$th term, that term and all the terms after it are within $0.000001$ of the limit.

In the technical language of mathematics, I have specified a closeness (here, I said $\epsilon = 0.000001$, but it could have been any number, so we just call it $\epsilon$) and you have found a point in the tail (here, you found $N=537$) after which all subsequent terms (all $a_n$ for $n\geq N$) are within my specified closeness of the limit (that is, $|a_n-a|<\epsilon$ for all $n\geq N$). Remember, numbers are "close" if their difference is small in absolute value.

Now, how did I know $a$ was the limit? I didn't. It's the DEFINITION of being the limit if it has that property (if you can find the tail when I give the closeness, no matter what closeness I give). And if it happens that the "$a$" is NOT the limit, you will find that there is indeed a value of $\epsilon$ I could specify for which NO TAIL, no matter how far out, stays close to $a$. This could happen if either the sequence actually converges to some OTHER number, or doesn't converge at all.

Addendum: Since I'm the one that gave you $\epsilon$, and you still have to find an $N$ whenever I give you an $\epsilon$, we say "for all $\epsilon$" (and of course $\epsilon>0$; if $\epsilon=0$, then that would require a sequence for which the tail is eventually constant with every term equal to $a$, not very interesting).

Answer 2

You can see it like a sort of game. Suppose we have the sequence $$ \frac12, \frac23, \frac34,\ldots,\frac{n}{n+1},\ldots. $$ Suppose you claim: "This sequence converges to the number 1." Suppose I claim: "No it doesn't!" So we play a game to see what happens. Since I think it doesn't converge to one, I'm going to try to give you a number so small, that you will never get that close to the number 1. For instance, I give you $\epsilon = \frac1{1000000}$. Then you say, "Oh, no problem -- if you just look at $a_{1000000}$, you'll see that indeed $a_{1000000}$ is within distance $\epsilon$ of $1$. That is, $$ |a_{1000000} - 1| < \epsilon." $$ If you can always win this game, no matter how small of an $\epsilon$ I give you, that is starting to sound an awful lot like the sequence converges to 1, right?

There is one subtle difference: consider the sequence $0,1,0,1,0,1,0,\ldots$. The way I described the game above, you could prove that this sequence converges to 0: it is easy to find terms $a_n$ that are within distance $\epsilon$ of $0$: any $0$ term in the sequence will do. Convergent sequences shouldn't just approach a value, they should stay there too. So rather than saying, "$a_{1000000}$ is very close (within epsilon) to $a$", you say, "starting at $1000000$, the sequence stays very close (within $\epsilon$) to $a$". That's where the $\forall n \geq N$ comes from.

Answer 3

For a sequence to converge, it has to be close to the value it is going to converge. How "close" is measured by $\epsilon$, and the speed at which the sequence approaches the limit is defined by $N$.

Similarly, if it doesn't get "close" enough, that is, there exists $\epsilon>0$ such that the inequality fails for all $N$, then it can't converge to that value of $a$.

If it can't converge to any $a$, it diverges.