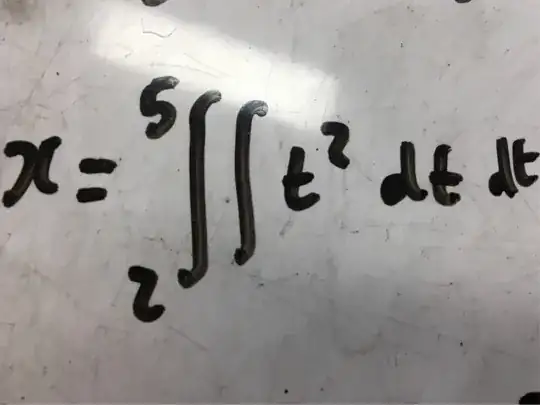Is there a better notation for integrating twice?

Question

I'm studying kinematics with varying acceleration. To calculate the displacement from the acceleration you have to integrate the acceleration with respect to t, then integrate that with respect to t, this time with limits.

I've been writing this:

But it looks a little messy. Is there a better way?

The notation on this webpage is good but seems to be aimed at having a) limits on both integrals (for me the inner integral is indefinite) and b) different variables - in differentiating with respect to t both times.

Answer 1

No, there is no better notation - the double-integral notation is standard. However, the way you've written it is problematic. Notice that when you do an indefinite integral, you get a $+c$ at the end. This is a constant, so when integrated again we have $+ct$. Evaluating from $2$ to $5$, this gives a $+3c$ at the end of your answer - which you really don't want, since your answer should be a number.

In a double integral, the inner integral should a) always be definite and b) be with respect to a different variable than the outer integral. In your case, recall that velocity is not the indefinite integral of acceleration - it's $v_0 + \int_0^ta(s)ds$, where $t$ is the time. So what you want is $\int_2^5\int_0^ts^2dsdt$.

This distinction between $s$ and $t$ is important - without it, you'll run into ambiguities as to which $t$ each $dt$ applies to.

Answer 2

This does not quite make sense to me, due to $$ \int t^2 \,dt = \frac 13 t^3 + C $$ Your integral just gives $$ \int_2^5 \int_t \tau^2 \, d\tau\, dt = \frac 1{12} (5^4 - 2^4) + 3C $$ for some arbitrary $C$, hence the result is just any(!) number. The result $23$ is as fine as $\pi$, just different and equally justified choices of $C$.

So I'd stick to an double integral with limits, so variable limits on the inner one. It is misleading to use the same integration variable twice, the standard way around is to use a "look-alike" variable name, for example the corresponding greek letter. So, a possibility is to write $$ \int_2^5 \left(u + \int_0^t \tau^2 \,d\tau\right) \, dt $$ where $u$ is the initial velocity. And if you want to stick to indefinite limits, I'd write $$ \int_2^5 \int_t \tau^2 \,d\tau \, dt $$

Answer 3

You want to write $F(t) = \int t^{2}\text{d}t$. This is equal to:

$F(t) = F(0) + \int_{0}^{t}s^{2}\text{d}s$ provided the expression is defined at $t=0$.

Then, you could write:

$$x = \int_{2}^{5}\left(F(0)+\int_{0}^{t}s^{2}\text{d}s\right)\text{d}t$$

In your case, you probably want $F(0)$ to be your initial velocity $v_{0}$. Hence, the above integral is:

\begin{align*} x &= \int_{2}^{5}\left(F(0)+\int_{0}^{t}s^{2}\text{d}s\right)\text{d}t\\ &= \int_{2}^{5}\left(v_{0}+\int_{0}^{t}s^{2}\text{d}s\right)\text{d}t\\ &= \int_{2}^{5}\left(v_{0} + \left[\frac{s^{3}}{3}\right]_{0}^{t}\right)\text{d}t\\ &= \int_{2}^{5}\left(v_{0} + \frac{t^{3}}{3}\right)\text{d}t\\ &= \left[v_{0}t + \frac{t^4}{12}\right]_{2}^{5}\\ &= v_{0}(5-2) + \frac{5^4}{12} - \frac{2^4}{12}\\ &= 3 v_{0} + \frac{609}{12} \end{align*}

(Corrected after TonyK's comment: I added the numbers instead of subtracting them).

Answer 4

But a definite integral of an indefinite integral has a big problem: it depends on the chosen primitive. Indeed, suppose that $F'(x)=f(x)$. Then $$\int_a^b\left(\int f\right)dx=\int_a^b (F(x)+C)dx=C(b-a)+\int_a^bF(x)dx$$ Are you sure that this is what you want?

Answer 5

You should have $\int \int a\; dt \; dt$, then the limits should be the same-both the start and end times of the acceleration. It can be confusing to use $t$ as the dummy variable and also to use the same dummy variable in both integrals. If we want the position as a function of time $t$ starting from $t_0$ with position $s_0$ and velocity $v_0$ we can use $\tau$ and $\tau'$ as dummy variables and we would get $$\int_{t_0}^t \int_{t_0}^{\tau'} \tau^2\; d\tau \; d\tau'=\int_{t_0}^t\left.\left(\frac 13\tau^3\right)\right|_{t_0}^{\tau'}\;d\tau'\\ =\int_{t_0}^t\frac 13(\tau'^3-t_0^3)\; d\tau'\\ =\frac 1{12}\tau'^4|_{t_0}^t-t_0(t-t_0)\\ =\frac 1{12}(t^4-t_0^4)-t_0(t-t_0)$$

Answer 6

If it was a pure mathematics, it would be OK. If it is kinematics, i.e. physics, it is absurd. In physics you need to track the physical quantities denoted by every expression and keep them consistent to make a reasonable calculations.

The expression $t^2$ is a physical quantity 'time squared', different from the acceleration's 'length divided by time squared'; the latter has an SI unit $m/s^2$ while the former is in $s^2$.

You need at least some constant $q$ in $m/(s^4)$ for a double integration $\int\int q t^2 \,dt\,dt$ to make any sense. And then, as others said, you need to carefully define limits of integration.

A distance $s$ travelled over time $T$ is an integral of a velocity over that time: $$s(T) = \int\limits_{t=T_0}^T v(t)\,dt $$ and a final position is an initial position $x_0=x(T_0)$ plus the distance: $$x(T) = x_0 + s(T)$$

Next, the velocity change over time follows from the acceleration, namely it's an integral of $a$: $$v(t) = v_0 + \int\limits_{\tau=T_0}^t a(\tau)\,d\tau$$ where $v_0=v(T_0)$ is the initial velocity.

Now plug $v(t)$ into the first equation: $$x(T) = x_0 + \int\limits_{t=T_0}^T \left(v_0 + \int\limits_{\tau=T_0}^t a(\tau)\,d\tau\right)\,dt $$

Add the acceleration definition and the integration expression is complete: $$x(T) = x_0 + \int\limits_{t=T_0}^T \left(v_0 + \int\limits_{\tau=T_0}^t q\tau^2\,d\tau\right)\,dt $$

Work it from inside out: $$\int q\tau^2\,d\tau = \frac 13 q\tau^3$$ so $$v(t) = v_0 + \int\limits_{\tau=T_0}^t q\tau^2\,d\tau = v_0 + \left[\frac 13q\tau^3\right]_{\tau=T_0}^t = v_0 + \frac q3(t^3-{T_0}^3)$$ then $$x(T) = x_0 + \int\limits_{t=T_0}^T \left(v_0 + \frac q3(t^3-{T_0}^3)\right)\,dt $$ $$= x_0 + \int\limits_{t=T_0}^T \left(v_0 + \frac q3 t^3- \frac q3 {T_0}^3\right)\,dt $$ $$= x_0 + \left[\frac q{12} t^4 + \left(v_0 - \frac q3 {T_0}^3\right)t\right]_{t=T_0}^T $$ $$= x_0 + \frac q{12} (T^4 - {T_0}^4) + \left(v_0 - \frac q3 {T_0}^3\right)(T-T_0) $$

Assuming your frame of reference has been chosen so that $x_0=0\,m$ and $v_0=0\,\frac ms$, the expression simplifies to $$x(T) = \frac q{12} (T^4 - {T_0}^4) - \frac q3 {T_0}^3 (T-T_0) $$ For $T=5\,s$ and $T_0=2\,s$: $$x(5\,s) = \frac q{12} ((5\,s)^4 - (2\,s)^4) - \frac q3 (2\,s)^3 (5\,s-2\,s) $$ $$ = \frac q{12} (625 - 16)s^4 - \frac q3 8\cdot 3\, s^4 $$ $$ = \left(\frac {625 - 16}{12} - 8\right)q\,s^4 $$ $$ = 42.75\, q\,s^4$$ If $q = 1\,\frac m{s^4}$, as I suppose from your attempt to write the double integral: $$ x(5\,s) = 42.75\,m$$