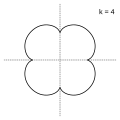
I am reading about epicycloids and I wonder if they are algebraic. Here is in polar coordinates:
\begin{eqnarray*} x(\theta) &=& (R+r) \cos \theta - r \cos \left( \frac{R+r}{r} \theta\right) \\ y(\theta) &=& (R+r) \sin \theta - r \sin \left( \frac{R+r}{r} \theta\right) \\ \end{eqnarray*}
Then is this curve algebraic? If I add the real and imaginary parts we obtain: $$ \theta \mapsto (R+r) e^{i\theta} - r e^{i\frac{R+r}{r} \theta} = (R+r) z - r z^{\frac{R+r}{r} } $$
Still is still not an equation of the type $f(x,y) = 0$. The cardioid has an equation:
$$ (x^2 + y^2 +ax)^2 = a^2 (x^2 + y^2) $$