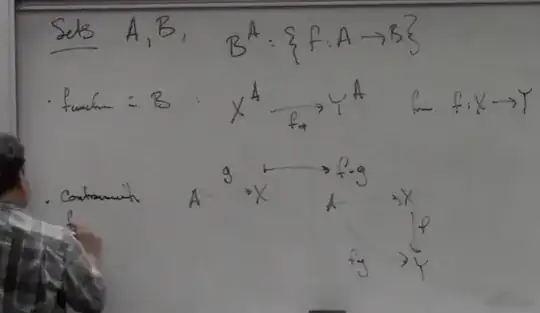1

I am following Awodey's category theory course and stuck at this example:

enter image description here

How is $X^A$ a category? What does "functor in argument B" mean? Could anyone please explain the diagrams in more detail? Sorry if I am asking a trivial question here, it's all very confusing to me at this point.

qed
  • 1,103

2 Answers2

3

Awodey is being what one might consider a bit too general here. Every set can be considered as a discrete category (one where identities are the only arrows). So the exponential $B^A$ of two sets is also the (discrete) functor category of $A,B$ thought of as categories. By describing this as a functor he's laying pipe for talking about induced functors between more general functor categories.

But the important thing in this example is that the $-^A:Set\to Set$ and $B^-:Set^{op}\to Set$ are functorial operations, the former of which is covariant and the latter of which is contravariant.

Ian
  • 104,572
Malice Vidrine
  • 9,843
  • What do you mean by saying that "the exponential $B^A$ of two sets is also the (discrete) functor category of $A,B$ thought of as categories." ? I ask also because I don't understand the second paragraph of Derek Elkins' answer here https://math.stackexchange.com/questions/2382194/what-is-the-carrier-set-functor/2382220#2382220 which seems to be related. – user65526 Aug 04 '17 at 10:37
  • @user65526 - Do you understand what it means to say that a set can be considered a discrete category? That is, for a set $A$, we form the category whose set of objects are just the elements of $A$, and whose only arrows are identities; let's denote this category with the same letter in calligraphic text, $\mathcal A$. Applying this construction to the set $B^A$ gives you a category that is isomorphic to the functor category $\mathcal{B}^\mathcal{A}$. – Malice Vidrine Aug 04 '17 at 14:34
  • I understand now thanks :) – user65526 Aug 04 '17 at 15:08
2

Being a functor in argument $B$ means that we fix $A$, so the functor will be between objects of the form $X^A$ and $Y^A$. If we had said "functor in argument $A$" instead, then we'd fix $B$ and consider functors between objects $B^X$ and $B^Y$.

How do we define such functors (focusing on the first kind we mentioned)? Well if we have an arrow $f:X\to Y$ (in the category of Sets), we get an induced functor $X^A\to Y^A$ given as follows: an object $\varphi\in X^A$ (i.e. a morphism $\varphi:A\to X$) gets mapped to $f\circ\varphi:A\to Y$, which we sometimes call $\varphi_*$.

Edit: okay, so let's reevaluate what is going on. It seems we are talking about a functor $F:\bf{Set}\to\bf{Set}$ (first, fixing $A$). How will we define $F(X)$? We will define $F(X)=X^A$. What is the action of $F$ on arrows? It takes an arrow $f:X\to Y$ to the arrow $F(f):X^A\to Y^A$, which is what we discussed in the above paragraph; this arrow takes an object $\varphi\in X^A$ to $f\circ\varphi\in Y^A$, i.e. $F(f)(\varphi)=f\circ\varphi$ (although this is not a nice looking way to write it). Note that $F$ is covariant.

Now, let's do the same thing but fixing $B$. That is, if we again call the functor $F$, then $F(X)=B^X$. The value on arrows this time? Well if we have an arrow $f:X\to Y$, then we get an induced map $B^Y\to B^X$ as follows: $\varphi\in B^Y$, i.e. $\varphi:Y\to B$ gets sent to $\varphi\circ f\in B^X$. Note then that this is indeed contravariant, since $f:X\to Y$ but $F(f):B^Y\to B^X$.

Sorry about the confusion there... I hope this helps. Let me know if there's anything I can clarify further.

TY Mathers
  • 19,533
  • I believe you mean "induced function $X^A \rightarrow Y^A$". – qaphla Dec 26 '16 at 15:35
  • @qaphla I don't think so. It is a functor $f\circ-:X^A\to Y^A$. – TY Mathers Dec 26 '16 at 16:29
  • Cool, this combined with the "discrete category" part from Malice's answer has given me a clear picture of the example. – qed Dec 26 '16 at 22:35
  • I have another question though. In the same video, there is another example on contravariant functor $f^* : B^Y \rightarrow B^X$, I understand it works by pre-composition $- \circ f$, but how is that contravariant? A functor F is called contravariant if it reverses the directions of arrows, I don't see how the arrows could be meaningfully reversed if the categories are discrete. – qed Dec 26 '16 at 22:40
  • I just looked at the video you linked (which I hadn't done before) and I don't think he is actually talking about $X^A$ as a discrete category. I'm going to edit my post to give a thorough explanation. @qaphla it looks like you were right, sorry about that – TY Mathers Dec 26 '16 at 22:49