Is the set $S = \{x \in [0, \infty)^2 \mid x_1 x_2^2 \leq 1\}$ convex?

Question

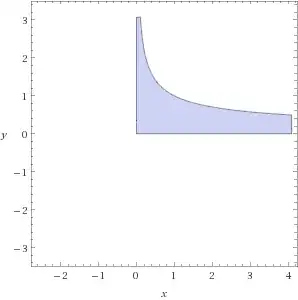
We have the function $\displaystyle{y=f(x_1, x_2)=x_1\cdot x_2^2}$ and the set $S=\{x\in [0, \infty)^2 \mid f(x_1, x_2)\leq 1\}$.

I want to check if the set is convex.

$$$$

Let $x=(x_1, x_2) , y=(y_1, y_2)\in S$, then $x_1\cdot x_2^2\leq 1$ and $y_1\cdot y_2^2\leq 1$.

We want to show that \begin{equation*}\lambda x+(1-\lambda )y=\lambda (x_1, x_2)+(1-\lambda )(y_1, y_2)=(\lambda x_1+(1-\lambda )y_1, \lambda x_2 +(1-\lambda )y_2)\in S\end{equation*} so we have to show that \begin{equation*}f\left (\lambda x_1+(1-\lambda )y_1, \lambda x_2 +(1-\lambda )y_2\right ) \leq 1\end{equation*}

We have the following: \begin{align*}f&\left (\lambda x_1+(1-\lambda )y_1, \lambda x_2 +(1-\lambda )y_2\right )=(\lambda x_1+(1-\lambda )y_1)\cdot( \lambda x_2 +(1-\lambda )y_2)^2 \\ &=(\lambda x_1+(1-\lambda )y_1)\cdot( \lambda^2 x_2^2+2\lambda x_2(1-\lambda )y_2 +(1-\lambda )^2y_2^2)\\ &= \lambda x_1\cdot( \lambda^2 x_2^2+2\lambda (1-\lambda )x_2y_2 +(1-\lambda )^2y_2^2)+(1-\lambda )y_1\cdot( \lambda^2 x_2^2+2\lambda (1-\lambda )x_2y_2 +(1-\lambda )^2y_2^2) \\ & = \lambda^3 x_1x_2^2+2\lambda^2 (1-\lambda )x_1 x_2y_2 +\lambda (1-\lambda )^2x_1 y_2^2+ \lambda^2 (1-\lambda )x_2^2y_1+2\lambda (1-\lambda )^2x_2y_1y_2 +(1-\lambda )^3y_1y_2^2 \\ & \leq \lambda^3 +2\lambda^2 (1-\lambda )x_1 x_2y_2 +\lambda (1-\lambda )^2x_1 y_2^2+ \lambda^2 (1-\lambda )x_2^2y_1+2\lambda (1-\lambda )^2x_2y_1y_2 +(1-\lambda )^3\end{align*}

Is this correct so far?

How could we continue?

$$$$

EDIT:

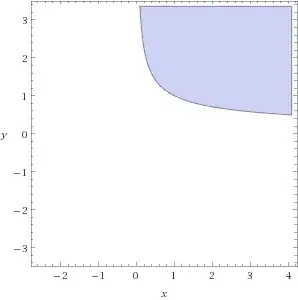
What about the set $\tilde{S}=\{x\in [0, \infty)^2 \mid f(x_1, x_2)> 1\}$ ?

Doing the same as above we get $$\ldots> \lambda^3 +2\lambda^2 (1-\lambda )x_1 x_2y_2 +\lambda (1-\lambda )^2x_1 y_2^2+ \lambda^2 (1-\lambda )x_2^2y_1+2\lambda (1-\lambda )^2x_2y_1y_2 +(1-\lambda )^3$$

How could we continue?

Answer 1

The set is not convex. Consider $x=(0,a),y=(a,0).$ Then

$$f(\lambda x+(1-\lambda)y)=f((1-\lambda)a,\lambda a)=(1-\lambda)\lambda^2a^3.$$ Consider $\lambda=1/2$ and $a^3=16.$ Then the expression takes the value $2>1.$ Note that $f(0,16)=f(16,0)=0\le 1.$

Answer 2

I would say, pick a couple of numbers that you know are on the boundary of your set.

$(4, \frac 12),(\frac 14,2)$ would be two such numbers. Now pick the midpoint of the line between these two points. $f(\frac {17}{8}, \frac {5}{4}) = \frac {17\cdot25}{8\cdot16} = \frac {425}{128}>1$

Not convex.

Answer 3

Let

$$\mathcal S_1 := \{ (x,y) \in (\mathbb R_0^+)^2 \mid x y^2 \leq 1 \}$$

$$\mathcal S_2 := \{ (x,y) \in (\mathbb R_0^+)^2 \mid x y^2 \geq 1 \}$$

Plotting $\mathcal S_1$, it is clear that it is non-convex.

Plotting $\mathcal S_2$, we obtain what looks very much like a convex set.

Note that $\mathcal S_2$ can be represented by the following linear matrix inequality (LMI)

$$\begin{bmatrix} x & 1 & 0\\ 1 & y^2 & 0\\ 0 & 0 & y\end{bmatrix} \succeq \mathrm O_3$$

Hence, $\mathcal S_2$ is a spectrahedron and, thus, convex.

---

convex-analysis linear-matrix-inequality spectrahedra