Let $\mathcal{A}$ be an abelian category and let $(X^\bullet, d^\bullet)$ be a chain complex in $\mathcal A$. I want to show that there exists an exact sequence $$0\to \text{im}(d^{i-1})\to \ker(d^i)\to H^i(X^\bullet)\to 0.$$ This is easy to show if $\mathcal{A}$ is the category of modules over a ring (for example), but it seems quite tedious to show in general. Any suggestions?
- 4,252
-
1What is your definition of $H^i(X^\bullet)$? The way I would define it, this is true by definition... – Eric Wofsey Dec 11 '16 at 23:53
1 Answers
If you want to prove it, then what is your definition of $H^i (X^\bullet)$?
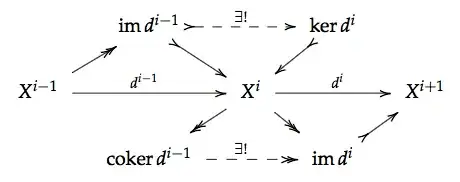
In an arbitrary abelian category, the definition is the following. First note that the condition that $X^\bullet$ is a complex, i.e. that $d^i\circ d^{i-1} = 0$ for all $i$, implies that we have a canonical mono $\operatorname{im} d^{i-1} \rightarrowtail \ker d^i$ and a canonical epi $\operatorname{coker} d^{i-1} \twoheadrightarrow \operatorname{im} d^i$ that give the following commutative diagram:
Then $$H^i (X^\bullet) := \operatorname{coker} (\operatorname{im} d^{i-1} \rightarrowtail \ker d^i) \cong \ker (\operatorname{coker} d^{i-1} \twoheadrightarrow \operatorname{im} d^i).$$
So that by definition, there are short exact sequences $$0 \to \operatorname{im} d^{i-1} \to \ker d^i \to H^i (X^\bullet) \to 0$$ and $$0 \to H^i (X^\bullet) \to \operatorname{coker} d^{i-1} \to \operatorname{im} d^i \to 0$$
-
P.S. OK, the list of related questions tells me this has been already asked: http://math.stackexchange.com/questions/18047/ – Dec 12 '16 at 00:03