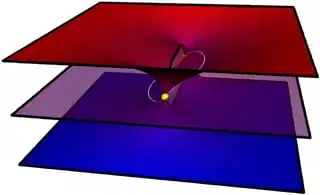
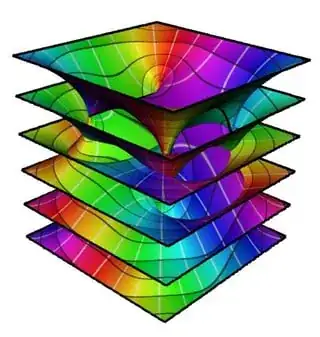
They draw nice pictures of Riemann Surfaces in "Automatic Generation of Riemann Surface Meshes" by Matthias Nieser, Konstantin Poelke, and Konrad Polthier:
Identify each layer with a vertex, then for the left it is easy to relate the Riemann surface with a graph: it is the cyclic graph with 3 vertices.
I'll try to explain: Think of the layers extended to infinity. Identify the a vertex with a point on a layer infinitely far way. Two points/vertex are connected if there is a transition between the two layers where the points live.
But how for more complicated Riemann surfaces like the right one? Is it (the other way round now) always possible to construct a Riemann surface for a given graph?