find the value of given trigonometric equation

Question

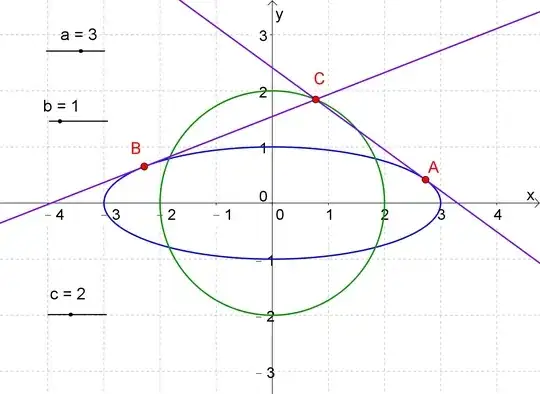
If $\alpha$ and $\beta$ are two different values of $\theta$ which satisfy $$bc \cos{​θ} \cos{\phi} + ac \sin{\theta} \sin{\phi} = ab,$$ then what is the value of $$(b^2 + c^2 - a^2) \cos{\alpha} \cos{\beta} + (c^2 + a^2 - b^2) \sin{\alpha} \sin{​\beta}\,?$$

Answer 1

Considering an ellipse

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

The equations of tangents at $[\alpha]$ and $[\beta]$ are

$$\frac{x\cos \alpha}{a}+\frac{y\sin \alpha}{b}=1$$

$$\frac{x\cos \beta}{a}+\frac{y\sin \beta}{b}=1$$

If the tangents meet at $(c\cos \phi, \, c\sin \phi)$, then

$$(c\cos \phi , \, c\sin \phi)= \left( a\frac{\cos \frac{\alpha+\beta}{2}}{\cos \frac{\alpha-\beta}{2}} \, , \; b\frac{\sin \frac{\alpha+\beta}{2}}{\cos \frac{\alpha-\beta}{2}} \right)$$

Refer to this link

I \begin{align*} \frac{c^2\cos^2 \phi}{a^2}+\frac{c^2\sin^2 \phi}{b^2} &= \sec^2 \frac{\alpha-\beta}{2} \\ \cos^2 \frac{\alpha-\beta}{2} &= \frac{a^2b^2}{c^2(a^2\sin^2 \phi+b^2\cos^2 \phi)} \\ \cos (\alpha-\beta) &= \frac{2a^2b^2}{c^2(a^2\sin^2 \phi+b^2\cos^2 \phi)}-1 \\ \end{align*}

II \begin{align*} \tan \frac{\alpha+\beta}{2} &= \frac{a}{b} \tan \phi \\ \cos (\alpha+\beta) &= \frac{1-\frac{a^2}{b^2} \tan^2 \phi}{1+\frac{a^2}{b^2} \tan^2 \phi} \\ &= \frac{b^2\cos^2 \phi-a^2\sin^2 \phi}{a^2\sin^2 \phi+b^2\cos^2 \phi} \end{align*}

III \begin{align*} E &= (b^2+c^2-a^2)\cos \alpha \cos \beta+ (c^2+a^2-b^2)\sin \alpha \sin \beta \\[5pt] &= c^2\cos (\alpha-\beta)+(b^2-a^2)\cos (\alpha+\beta) \\[5pt] &= \frac{a^4\sin^2 \phi+a^2b^2+b^4\cos^2 \phi} {a^2\sin^2 \phi+b^2\cos^2 \phi}-c^2 \\[5pt] &= \frac{a^4\sin^2 \phi+ a^2b^2\color{red}{(\sin^2 \phi+\cos^2 \phi)}+ b^4\cos^2 \phi} {a^2\sin^2 \phi+b^2\cos^2 \phi}-c^2 \\[5pt] &= \fbox{$a^2+b^2-c^2$} \end{align*}

Note Briefly:

• For real distinct $\alpha$ and $\beta$, $$c > \frac{ab}{\sqrt{a^2\sin^2 \phi+b^2\cos^2 \phi}} \ge \min(a,b) > 0$$

• If $c^2=a^2+b^2$, then $x^2+y^2=c^2$ is the director circle of the ellipse so that $AC \perp BC$.

Answer 2

Hint:

$$(ab-ca\sin\theta\sin\phi)^2=(bc)^2\cos^2\phi(1-\sin^2\theta)$$

Rearrange to form a quadratic equation in $\sin\theta$

Now use Vieta's formula to find $\sin\alpha\sin\beta$

Similarly for cosine.