Find the value of $z_1^2 + z_2^2 + z_3^2$ given that $z_1, z_2, z_3 \in \mathbb{C}$, $z_1 + z_2 + z_3 = 0$ and $|z_1| = |z_2| = |z_3| = 1$.

Question

So I'm given the task of finding the value of $$z_1^2 + z_2^2 + z_3^2$$ For $z_1, z_2, z_3 \in \mathbb{C}$ such that $z_1 + z_2 + z_3 = 0$ and $|z_1| = |z_2| = |z_3| = 1$.

(Edit: of course $|z|$ represents the modulus of $z$)

I have done some manipulations but have arrived at nothing which I consider to be useful. If anyone can guide me, I'd be very thankful.

[I'm aware there is a question which is very similar and speaks of the fact that $z_1, z_2$ and $z_3$ are the points of an equilateral triangle although I do not see a correlation with this problem, so as a side request, if this has to do with that, I'd also appreciate to understand why, although this is more out of curiosity]

Answer 1

$$0 = \bar{z_1}\bar{z_2}\bar{z_3}(z_1+z_2+z_3) = \bar{z_2}\bar{z_3}+\bar{z_3}\bar{z_1}+\bar{z_1}\bar{z_2}$$ and hence $$z_1z_2 + z_2z_3 + z_3z_1 = 0$$ Now $$0 = (z_1 +z_2+z_3)^2 = z_1^2 + z_2^2 +z_3^2 + 2(z_1z_2 + z_2z_3 + z_3z_1)$$ and thus $$z_1^2 + z_2^2 + z_3^2 = 0$$

Answer 2

(Not an answer proper, but too long for a comment.)

I'm aware there is a question which is very similar and speaks of the fact that $z_1 ,z_2$ and $z_3$ are the points of an equilateral triangle although I do not see a correlation with this problem

The respective question is Vertices of equilateral triangle inscribed in the unit circle which states:

Prove that if $z_{1}+z_{2}+z_{3}=0$ and $|z_{1}|=|z_{2}|=|z_{3}|=1$ then the points $z_{1},z_{2},z_{3}$ are the vertices of an equilateral triangle inscribed in the unit circle $|z|=1$.

Your question is directly equivalent to the other one, and both are equivalent to proving that $z_1 z_2 + z_2 z_3 + z_3 z_1 = 0$ so that $z_k$ are the roots of a cubic $z^3-w=0$ with $|w|=1$.

I don't see a direct proof to your problem which wouldn't at some point derive and use the fact that $\triangle Z_1Z_2Z_3$ is equilateral, or $z_k = z_1 \omega_k$ where $\omega_k$ are the cube roots of unity.

Answer 3

Think geometrically about how $3$ numbers in the unit circle could sum $0$. Assuming some familiarity with the complex plane one should soon get the easy solution $$ S_0=\{1,e^{i\frac{2\pi}{3}},e^{-i\frac{2\pi}{3}}\}. $$ After this one rapidly generalizes to $$ S_\theta=e^{i\theta}S_0=\{e^{i\theta},e^{i(\theta+\frac{2\pi}{3})},e^{i(\theta-\frac{2\pi}{3})}\}. $$ Graphically:

                                  

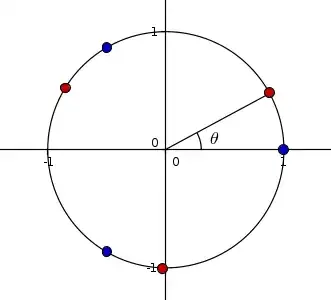
(The three blue dots are the elements of $S_0$, and the three red points the elements of $S_\theta$).

So we have a parametric family of solutions of $z_1+z_2+z_3=0$ in the unit circle. Are there other solution $S$ to this problem that is not of this form? No: If $S$ is not of this form then there are two elements $e^{i\alpha}, e^{i(\alpha+\beta)}\in S$ with $\beta\neq \pm\frac{2\pi}{3}$. Call $w$ the other element of $S$. As the sum of the elements of $S$ must be $0$ we must have $$ -w=e^{i\alpha}+e^{i(\alpha+\beta)}, $$ so the RHS must have modulus equal to one $1$. Calculating \begin{align} |e^{i\alpha}+e^{i(\alpha+\beta)}|^2=&(\cos\alpha+\cos(\alpha+\beta))^2+(\sin\alpha+\sin(\alpha+\beta))^2\\=&\underbrace{\cos^2\alpha+\cos^2\beta}_{1}+\underbrace{\cos^2(\alpha+\beta)+\sin^2(\alpha+\beta)}_{1}+2\underbrace{(\cos\alpha\cos(\alpha+\beta)+\sin\alpha\sin(\alpha+\beta))}_{\cos\beta}. \end{align}

we arrive at $1^2=2+2\cos\beta\hspace{.1cm}$; i.e. $\cos\beta=-\frac{1}{2}$ which only holds if $\beta=\pm\frac{2\pi}{3}$.

So every solution to $z_1+z_2+z_3=0$ in the unit circle is $S_\theta$ for some $0\leq\theta<2\pi$. This reduces your question to $$\text{"if $S_\theta=\{w_1,w_2,w_3\}$, then what is the value of $w_1^2+w_2^2+w_3^2$ ?",}$$ which becomes obvious with the observation that $$(z\mapsto z^2)(S_\theta)=S_{2\theta}.$$ I.e. $S_{2\theta}=\{w_1^2,w_2^2,w_3^2\}$, which is a solution of $z_1+z_2+z_3=0$. !!