6

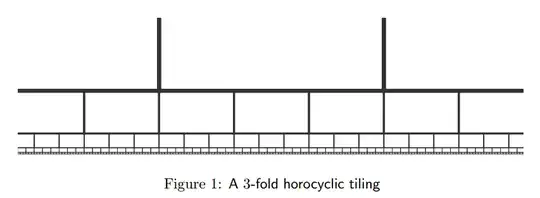
Has anyone produced a quasiperiodic tiling of the hyperbolic plane?

Or is there a reason it cannot be done?

By quasiperiodic I mean that the structure is not strictly periodic (i.e. equal to itsef after translation) but that any arbitrary large neighbourhood of any point can be found identically at an infinity of other locations.

Descartes Before the Horse
  • 7,386
Florian F
  • 495

1 Answers1

2

Yes, this question has been somewhat studied, for instance by Chaim Goodman-Strauss. See this paper of his. See also this paper and references in both. Below is an image from the second paper which gives the first step in building a strongly aperiodic set of tiles in the hyperbolic plane, which I think Chaim would be ok with me copying here.

enter image description here

Perhaps one of the most important points brought up in this work is that the notion of aperiodicity or quasiperiodicity in the hyperbolic setting is more subtle than in the Euclidean case, and one should be careful with the definition being used (thus the use of 'weakly aperiodic' and 'strongly aperiodic').

Dan Rust
  • 30,973
  • Thanks for the links. Even though you do answer the question, it is not exactly what I was expecting. This tiling is periodic but with labels added that make it aperiodic. It is a bit technical. I was looking for something like the penrose tiling where the local 5-fold symmetry creates conflicts that forces the aperiodicity. I should have been more specific. – Florian F Nov 02 '16 at 08:22
  • No, this tiling is not periodic. Well, to be honest, one can construct this type of tiling to have a very limited periodicity, with respect to a vertical translation. However, that is the most periodicity that this type of tiling can have. Furthermore with just the slightest care it is also straightforward to construct this type of tiling having no periodicity whatsoever. – Lee Mosher Nov 02 '16 at 15:30
  • There is a sense in which Penrose-like tilings cannot exist, though it is also probably not in the sense that you mean. The Penrose tilings are an example of primitive substitution tilings (there are several ways to construct Penrose tilings, this is just one), and Bedaride and Hilion showed that no such primitive substitutions can exist which tile the entire hyperbolic plane - preprint. although they give examples of non-primitive substitutions which do work – Dan Rust Nov 02 '16 at 16:03
  • Yes, knew that the "fractal" construction principle of the Penrose tiling doesn't work well in the hyperbolic plane, because you cannot scale the pattern as the method would require. I was referring to the look of it, more uniform, with no direction singled out, and this balance between regularity and irregularity. – Florian F Nov 02 '16 at 20:12
  • @LeeMosher You are right. I wrongly assumed a horizontal translation of the half-plane is a translation in hyperbolic space. It is still highly symmetric via isometric transforms. – Florian F Nov 02 '16 at 20:25
  • How do we define periodicity when it comes to hyperbolic tilings? It looks to me like if you "zoom in" by a factor three on the $y=0$ line in this upper half plane model, you would get the same picture. I.e., if you performed the mapping $z\to 3z$, you would get back the same picture. Doesn't this make it periodic? – HelloGoodbye Mar 08 '23 at 01:31
  • If nothing else, it's very boring. So then the obvious million dollar question is, is there any quasiperiodic, interesting tiling of the hyperbolic plane? – HelloGoodbye Mar 08 '23 at 01:37