1

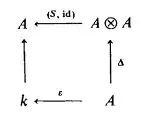
In this page they define the antipode using the diagram

enter image description here

I am finding it difficult to understand what is going on. In partiulcar:

  1. What is one the naked arrow going $k \to A$?

  2. Shouldn't the top arrow go $S \otimes A : A \otimes A \to A \otimes A$? I mean, if we start with $a \in A$, we should go: $a \mapsto \Delta(a) = \sum_a a_{(1)} \otimes a_{(2)} \mapsto \sum_a S(a_{(1)}) \otimes a_{(2)}$ and that should equal $a \mapsto u(a)$ how?

  • Normally $S$ is a linear map satisfying $\nabla(S\otimes id)\Delta=\eta\epsilon$ and $\nabla(id\otimes S)\Delta=\eta\epsilon$. If such a map exists, it is easy to show it is unique. – Ben Sheller Oct 28 '16 at 18:58
  • You should add some context - this way, one has to guess what the objects you are working with are. But from the book you are referencing, it seems that $A$ is the coordinate ring (=global sections) of an affine group scheme $G$; then the map $k \rightarrow A$ would be the arrow induced by the structure map $G \rightarrow \mathrm{Spec} ;k$ that makes $G$ into a scheme over $k$; in other words, it is the embedding ofthe field $k$ to $A$, making $A$ a $k$-algebra. Similarly, $S$ is induced by the inverse operation on $G$. The map $(S, \mathrm{id})$ is then given by $a\otimes b \mapsto S(a)b$. – Pavel Čoupek Oct 28 '16 at 18:58
  • see also: http://math.stackexchange.com/a/1980032/195021 – KonKan Oct 29 '16 at 14:30

1 Answers1

3

  1. Since $A$ is a $k$-algebra, the arrow $k \to A$ is the unit (sometimes written $\eta$) - the unique $k$-algebra morphism (it maps a scalar $t \in k$ to $t1 \in A$).

  2. Since $A \otimes A$ is the coproduct (in $k$-algebras) of $A$ and $A$, the two maps $S, \operatorname{id} \colon A \to A$ define a unique map from the coproduct $A \otimes A \to A$. This is the map denoted $(S,\operatorname{id})$; it maps $a \otimes b$ to $S(a)b$.

So the statement that the square commutes is just that, if $a \in A$ and $\Delta(a) = \sum_i a_i \otimes b_i$, then $$ \sum_i S(a_i)b_i = \epsilon(a)1, $$ as explained on the following page.

arkeet
  • 7,970