6

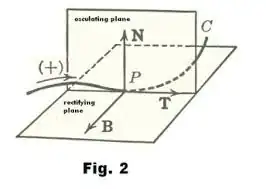
In studying calculus of space curves, we calculate the quantities "curvature" ($\kappa$) and "torsion"($\tau$). Both have inverse-length as units, so their reciprocals $\frac{1}{\kappa}$ and $\frac{1}{\tau}$ have units of length, and are called "radius of curvature" and "radius of torsion".

I understand that radius of curvature is the radius of a curve's osculating circle at a point. That's is a pretty clear notion geometrically, but I struggle to obtain a corresponding notion for radius of torsion.

Can anyone share a geometric intuition behind this length, and what it tells us about a non-planar curve? According to http://mathworld.wolfram.com/OsculatingSphere.html, the osculating sphere does not have radius $\frac{1}{\tau}$, so it's not that. Calling it a "radius" seems to imply that it's a radius of something.

Thanks in advance for any insight.

Edit: If a helix is given by $\left<a\cos t,a\sin t,bt\right>$, ($a$ and $b$ positive), then the curvature is $\frac{a}{a^2+b^2}$ and the torsion is $\frac{b}{a^2+b^2}$. There's a lovely duality there, and if you define a dual helix by swapping $a$ and $b$, then the curvature of one is the torsion of the other, and vice versa. Thus, we could say that the radius of torsion is the radius of curvature for a "dual" helix, but I hesitate to define a whole new kind of duality just to awkwardly impart meaning to a phrase I saw in a book. I don't know whether people who know a lot about helices think this way.

I'm still hoping there's a more natural answer out there.

G Tony Jacobs
  • 32,044
  • 1
    Where did you see the term "radius of torsion" used? This is the first I'm hearing about it. – Jesse Madnick Sep 23 '16 at 05:07
  • 2
    If you look up "torsion of a curve" on Wikipedia or Mathworld, it's defined in both articles. – G Tony Jacobs Sep 23 '16 at 05:09
  • There is an animation on Wikipedia which might help understanding the meaning of torsion, https://en.wikipedia.org/wiki/Torsion_of_a_curve – Thomas Sep 23 '16 at 05:18
  • 1
    That animation is great for understanding torsion as a measurement of how fast the binormal vector rotates about the tangent vector, but it doesn't really illuminate what "radius of torsion" represents, as a length. – G Tony Jacobs Sep 23 '16 at 05:27
  • There's osculating sphere which has third order of contact with the curve. – Ng Chung Tak Sep 23 '16 at 08:11
  • Yeah, it's radius isn't $1/\tau$, though. I mentioned that in my question. – G Tony Jacobs Sep 23 '16 at 10:52
  • 5
    I've worked in differential geometry my whole life and have never before come across this term. I do not see an interpretation other than by analogy with the definition of radius of curvature. Here's something a bit better: The mapping to the unit sphere given by $T(s)$ is called the tangent indicatrix; that given by $B(s)$ is called the binormal indicatrix. The speed of the tangent indicatrix is $\kappa$ and the speed of the binormal indicatrix is $\tau$. Perhaps someone sees something to get out of this ... – Ted Shifrin Sep 23 '16 at 17:22
  • Well, in a book called "vector analysis" the authors defined "the quantity 1/τ , which is denoted by Σ ,is called the radius of torsion".Also a question in that book says that for a helix [κΣ= constant].This is the use of "radius of torsion" according to the author. – Nothing Jan 02 '25 at 14:34

1 Answers1

3

I had also came across the notion of "radius of torsion" in the context of a lecture on Frenet-Serret system of equations, and had great difficulties in trying to conceptualize it. The notion of "radius of torsion" is a little more abstract then the "radius of curvature", and cannot be given a direct geometric interpretation as in the case of the letter. One reason for this difference is that torsion cannot exist without curvature; if one tries to define a space curve with non-zero torsion but zero curvature, then the torsion degenerates into curvature.

However, great background and guidance is given to this subject simply by reading a little about the history of differential geometry of space curves. Much earlier than the publication of Frenet-Serret formulas, Alexis Clariault reffered to general space curves as "curves of double curvature". This simple renaming gives some clue about conceptualization of torsion and curvature of general space curves.

Interpretation:

Assume $\gamma$ is a space curve traced by a point particle. Let $TN$ be it's local osculating plane at some point $X$ (the plane spanned by the tangent vector $T$ and the normal vector $N$), and $BT$ also be a local plane perpendicular to it (it's the plane spanned by the tangent vector $T$ and the binormal vector $B$. Now, let us project the curve $\gamma$ into each of the planes $TN$ and $BT$. One can do this simply by illuminating on the particle from the (local) $B$ and $N$ directions, and then looking at the curves which the particle's shadow traces in each plane.

Obviously, the local curvature of the curve traced by the shadow in the $TN$ plane is $\kappa$. In the same way, the local curvature of of the curve traced in the $TB$ plane is the torsion $\tau$; this gives a straightforward interpretation of the "radius of torsion" - this is radius of the circle which has second order contact with the projection of $\gamma$ into the local $TB$ plane.

A partial illustation of this interpretation can be seen in this picture; it shows the osculating ($TN$) plane and the $BT$ plane.

enter image description here

Caution:

I have not proved yet this claim with full rigourosity; but but nevertheless i wrote it down to make some contribution to the resolution of this question. I think that proving this claim will be my final attempt before i give up the attempts to gain intuition about the "radius of torsion" (and i hope my claim is correct!).

user2554
  • 1,228
  • This is amazing, especially after waiting almost three-and-a-half years! Thank you so much. I'll probably accept this answer later today, but I want to read it more carefully first. Cheers! – G Tony Jacobs Mar 11 '20 at 20:52
  • Thanks! but first you should really read my answer carefully, since i really didn't intend this answer to be the concluding remark on the notion of "radius of torsion". This is not a ripe conception, and i myself need to proccess it a bit more in my mind. – user2554 Mar 11 '20 at 20:59
  • 1
    I think it will be better to attempt to conceptualize the notion of radius of torsion of space curve using the "osculating sphere" instead of a Gauss's mapping (and then project it into the tangent plane), but i'm still exploring this concept. I'll update my answer if there will be any advances. – user2554 Mar 12 '20 at 10:16
  • 1
    Unfortunately, this is not correct. From the Frenet equations you can derive the local canonical form (assuming the curve is $C^3$ or better). The projection in the $TB$-plane (rectifying plane) looks like $$(u+o(u^2), (\kappa_0\tau_0/6)u^3 + o(u^3)).$$ Indeed, it's called the rectifying plane because this projection flattens the curve to have zero curvature at the point. P.S. Both $1/\kappa$ and $1/\tau$ show up in the radius of the osculating sphere, but sadly the $1/\tau$ is multiplied by $(1/\kappa)'$. – Ted Shifrin Mar 13 '20 at 16:16
  • After reading your comment i went to wikipedia and saw that the projection into the TB plane really traces a cubic polynomial. So i'm sorry i was eventually unable to help... it's really an interesting question how to give a meaningful interpretation to the "radius of torsion". – user2554 Mar 13 '20 at 16:38