Non-trivial questions about confocal ellipses

Question

This question arises from an attempt to give an elementary solution to an interesting problem.

Main question. Assume that $\Gamma_{AB}$ and $\Gamma_{AC}$ are two ellipses with foci at $A,B$ and $A,C$ respectively, meeting at $P$. Let $Q$ be the other point of intersection of $\Gamma_{AB}$ and $\Gamma_{AC}$: how to construct $Q$ with straightedge and compass, given $A,B,C,P$?

My attempt was to write the equation of both ellipses in polar coordinates and perform some trigonometry, but that does not translate easily into a simple straightedge and compass construction. So I wondered about some hidden projective property of two confocal ellipses, and indeed something striked me.

Secondary question. In the previous configuration, let $U$ be the pole of $PQ$ with respect to $\Gamma_{AB}$, i.e. the intersection of the tangents at $P$ and $Q$, and let $V$ be the pole of $PQ$ with respect to $\Gamma_{AC}$. Then $A$ lies on $UV$.

I was not able to prove this fact, but I discovered many interesting theorems in this Dolgirev paper, and I believe his techniques solves both the secondary question and the main question. May I ask some help from you, guys?

Answer 1

Construction.

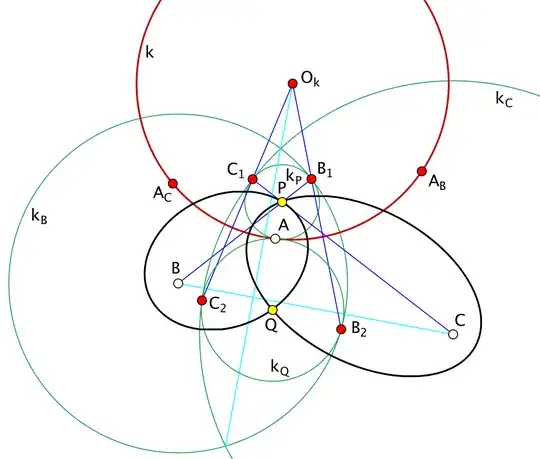
Draw circle $k_P$ centered at point $P$ and of radius $PA$. Draw circle $k_B$ centered at point $B$ and of radius $BP + PA$, and draw circle $k_C$ centered at point $C$ and of radius $CP + PA$. By construction $k_B$ is tangent to $k_P$ and let $B_1$ be the point of tangency (then $B_1 \, \in \, BP$). Also by construction $k_C$ is tangent to $k_P$ and let $C_1$ be the point of tangency (then $C_1 \, \in \, CP$). Construct the point $A_B$ as the inverse image of $A$ with respect to the circle $k_B$ and the point $A_C$ as the inverse image of $A$ with respect to circle $k_C$. Draw the circle $k$ as the circle passing through the three points $A, \, A_B$ and $A_C$. By construction $k$ is mapped to itself (not pointwise, but as a set) by inversion with respect to either of the circles $k_B$ and $k_C$, which means that $k$ is orthogonal to both $k_B$ and $k_C$ simultaneously. Determine the center of $k$ and denote it by $O_k$. By the way, due to the latter fact, $O_k$ lies on the radical axis of $k_B$ and $k_C$, which is the line formed by the two intersection points of $k_B$ and $k_C$ -- a line which is orthogonal to segment $BC$. By the orthogonality between $k$ and $k_B$ whenever one performs an inversion with respect to $k$, circle $k_B$ is mapped to itself. Analogously, circle $k_C$ is mapped to itself by inversion in $k$. Invert points $B_1$ and $C_1$ in $k$ to obtain their respective images $B_2$ and $C_2$. They necessarily lie on the circles $k_B$ and $k_C$ respectively and also on the straight lines $O_kB_1$ and $O_kC_1$ (i.e. $B_2 = O_kB_1 \cap k_B$ and $C_2 = O_kC_1 \cap k_C$ ). Thus, the inverse image with respect to $k$ of circle $k_P$ is the circle $k_Q$ passing thorugh points $A, \, B_2$ and $C_2$ and since $k_P$ is tangent to both $k_B$ and $k_C$, its image $k_Q$ is also tangent to $k_B$ and $k_C$ and the corresponding points of tangency are $B_2$ and $C_2$. Cosntruct the center of $k_Q$ and call it $Q$. This point $Q$ is the second intersection point of the two ellipses. 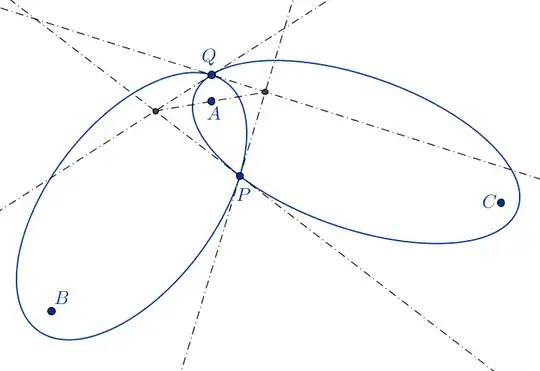Indeed $$BQ + QA = BQ + QB_2 = BP + PB_1 = BP + PA $$ $$CQ + QA = CQ + QC_2 = CP + PC_1 = CP + PA $$ Tangents. Denote by $\Gamma_{AB}$ the ellipse with foci $A$ and $B$ and passing through $P$ (and thus through $Q$). Denote by $\Gamma_{AC}$ the ellipse with foci $A$ and $C$ and passing through $P$ (and thus through $Q$).

Let $t_{AB}(P)$ be the tangent to $\Gamma_{AB}$ at point $P$. Then by the reflection property of rays trhough the foci of ellipses, the angle $\angle \,\, BP \, t_{AB}(P) = \angle \,\, AP\, t_{AB}(P)$ which means that $\angle \,\, B_1P\, t_{AB}(P) = \angle \,\, AP \, t_{AB}(P)$ i.e. $t_{AB}(P)$ is the bisector of angle $APB_1$. But since triangle $AB_1P$ is isosceles with $PA = PB_1$, the tangent $t_{AB}(P)$ is orthogonal to $AB_1$ and passes through the midpoint of segment $AB_1$. Absolutely analogous chain of arguments leads to the conclusion that the tangent $t_{AB}(Q)$ to $\Gamma_{AB}$ at the point $Q$ is orthogonal to segment $AB_2$ and passes through the midpoint of $AB_2$.

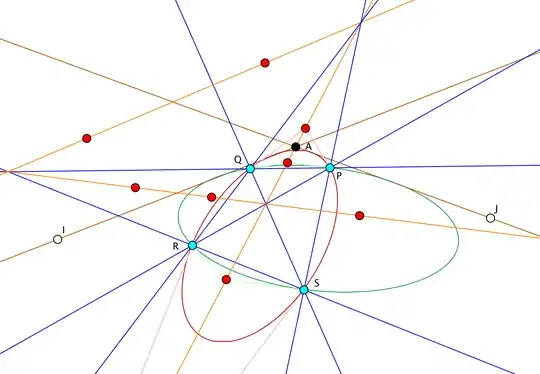
Now, let us look at the circle $k_{AB}$ defined by the three points $A, \, B_1$ and $B_2$. Then since $B_1$ and $B_2$ are inversive of each other with respect to circle $k$ and $A \in k$, circle $k_{AB}$ is orthogonal to circle $k$. Observe that $t_{AB}(P)$ is the orthogonal bisector of segment $AB_1$ and $t_{AB}(Q)$ is the orthogonal bisector of segment $AB_2$ which means that the intersection point of the two tangents $U = t_{AB}(P) \cap t_{AB}(Q)$ is in fact the center of circle $k_{AB}$. The orthogonality of circles $k$ and $k_{AB}$ is equivalent to the fact the radii $UA$ and $QA$ are orthogonal, i.e. $\angle \,\, UAQ = 90^{\circ}$.

Let $t_{AC}(P)$ be the tangent to $\Gamma_{AC}$ at point $P$ and let $t_{AC}(Q)$ be the tangent to $\Gamma_{AC}$ at point $Q$. Just as before, $t_{AC}(P)$ and $t_{AC}(Q)$ are orthogonal segment bisectors of segments $AC_1$ and $AC_2$ respectively. Then the circle $k_{AC}$ through $A, \, C_1$ and $C_2$ is again orthogonal to $k$ and the two tangents $t_{AC}(P)$ and $t_{AC}(Q)$ pass through the center of $k_{AC}$, which we denote by $V = t_{AC}(P) \cap t_{AC}(Q)$. The orthogonality of circles $k$ and $k_{AC}$ is equivalent to the fact that the radii $VA$ and $QA$ are orthogonal, i.e. $\angle\,\, VAQ = 90^{\circ}$. Thus, each of the two lines $AU$ and $AV$ passes through the point $A$ and is orthogonal to line $QA$, which means that these two lines coincide, i.e. $A$ lies on the line $UV$.

I hope I haven't made too many typos :D ...

Answer 2

This is not an answer. It's just too long and too illustrated for a comment.

I prefer to do most of my projective geometry over $\mathbb C$, so I'll be viewing the problem from this point of view. What does it mean for a point $A$ to be a focus of a given conic? It means that the lines joining $A$ to the ideal circle points $I=[1:i:0]$ and $J=[i:1:0]$ are tangents to the conic. So when you are talking about a pair of two confocal conics, then a more general description would be speaking about a pair of conics sharing two tangents. The common focus $A$ is the point where these tangents intersect. To make this easier to imagine, for the following picture I drew the points $I$ and $J$ at real positions. The brown lines are common tangents for the red and the green conic.

As Piquito pointed out, two conics will in general have four points of intersection. In the case of confocal ellipses it might well be that two of them have to be complex. But in the illustration above, all four of them are real.

If you pick the correct pair $P,Q$, then the line joining their poles does indeed pass through $A$, as you claimed. The same is true for the opposite pair of intersections, namely $R,S$. Their poles lie on the same line as those for $P,Q$. For other pairs of intersection, however, that is not the case. The other poles (red points) lie on two different lines (orange), four poles on each (not all of which are visible in the section above).

At this point I don't know how this may help you. Perhaps the most valuable property here might be the fact that the line joining the poles of $PQ$ is concurrent with the lines $PS$ and $QR$. Since $R$ and $S$ are complex in your setup, that does not lead to an obvious construction, but it might help with a proof for your second question. The fact that you have to match things correctly may make an algebraic proof somewhat complicated, though.