3

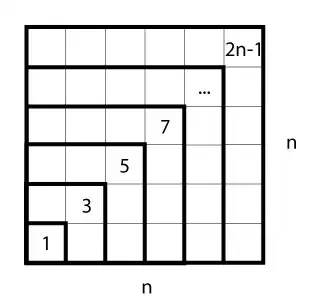
I have been thinking about this for a long time, may I know which step of my thinking is wrong as I do not seems to get the correct answer. If I am not going towards the right direction, may I get some help thanks!

My attempt:

Let $S = 1+3+5+\dotsb+(2n+1)\label{a}\tag{1}.$

Then I rearrange S from the last to first terms:

$S = (2n+1)+(2n-1)+(2n-3)+\dotsb+1\label{b}\tag{2}.$

Adding the two series $(1)+(2)$:

$$2S = (2n+2)+(2n+2)+(2n+2)+\dotsb+(2n+2),$$

I have $n$ copies of $(2n+2)$.

Therefore:

$2S = n(2n+2)$

$S = n(n+1)$.

Martin Sleziak
  • 56,060
user292965
  • 261

7 Answers7

3

enter image description here

Build a square in the following manner. On your first step, place $1$ block. On your second step put $3$ blocks around that, and on your third step put $5$ blocks around what you have, and so on. I think it should be pretty easy to see that the sum of the blocks is the area of the square for the step you are on.

In other words, the sum of the first $n$ odd integers is

$$ (2(1) - 1) + (2(2) - 1) + \dotsb + (2(n) - 1) = n^2. $$

Image source: google "sum of first $n$ odd numbers."

Alex Ortiz
  • 26,211
2

The last of $n$ numbers starting from $1, 3, 5, \ldots$ is $2n-1$, not $2n+1$. Replace accordingly and you should obtain the right answer.

Brian Tung
  • 35,584
2

$$S=1+3+5+7+\cdots 2r+1$$ $$S=2r+1 +2r-1+2r-3+2r-5+2r-7 +\cdots 1 $$ $$2S=2(2r+1)+r(2r)$$ $$S=r^2+2r+1=(r+1)^2$$ Instead of $r^{th}$ term you have written $(r+1)^{th}$ term.

This can also be verified using $$a_r=a + (n-1)d$$ $$a_r=2r-1 \qquad a_{r+1}=2r +1 $$ You can do it easily by this

We got genral term as $(2r-1)$ $$\sum_{r=1}^n2r-1$$ $$2\sum_{r=1}^n r-\sum_{r=1}^n1$$

Aakash Kumar
  • 3,576
0

Only have $n-1$ numbers of (2n+2)

therefore:

2S = (n-1)(2n+2)

S = (n-1)(n+1)

Reason:

when $n=1$, then first term is 3 rather than 1. Therefore, you only have $n-1$ numbers of (2n+2).

Zou lang
  • 1
  • If you do a couple of examples, you'll see that $S$ is always a perfect square, not one less than a square, which is what the formula $S=(n-1)(n+1)=n^2-1$ gives. – Barry Cipra Aug 19 '16 at 16:12
0

It is very simple, the sequence 1,3,5,........(2n+1) is arithmetic sequence having first term let say f = 1, last term say l = (2n+1) and common difference d = 2 , {(3-1),(5-3)......so on} and the sequence have n+1 terms so it can be represented as 1,3,5,..........(2n-1),(2(n+1)-1)

we can use formula for sum of arithmetic sequence having first term(f), last term(l) and total number of terms(n) as:

sum = n(f+l)/2

so, sum = (n+1)(1+2n+1)/2

      = (n+1)(n+1)
      = (n+1)^2

Hope it helps.......

Bishnu Basyal
  • 11
  • maths is hard to read if not formatted well, So please learn the basics here, http://meta.math.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference –  Aug 19 '16 at 17:25
0

$$1+3+5+\cdots+(2n+1) = \sum_{k=0}^n (2 k + 1) = 2 \binom{n+1}{2} + (n+1) = (n+1)^2$$

Rodrigo de Azevedo
  • 23,223
0

$$S=\sum^n_{k=1} (2n-1) \implies \sum^n_{k=1} 2n- \sum^n_{k=1} 1 \implies {2(n)(n+1)\over2} - n \implies n^2+n-n\implies n^2$$