How to plot the PSD cone in MATLAB

Question

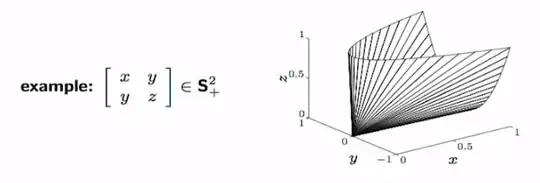
Does anybody know how I can plot in MATLAB the cone of positive semidefinite matrices as shown in the figure below? Thanks.

PSD cone

Answer 1

It is slightly easier to work on (symmetric) Positive Definite Matrices.

Such matrices

$$\begin{pmatrix} x & y \\ y & z \end{pmatrix}$$

are characterized by the double property:

$$x>0 \ \ \text{and} \ \ xz-y^2>0$$

(positivity of the principal minors).

Such matrices, when considered as points $(x,y,z) \in \mathbb{R^3}$, define a domain which is the interior of the half-cone with equation

$$y=\pm \sqrt{xz} \ \ \text{for} \ \ (x,z) \in (0,+\infty)^2$$

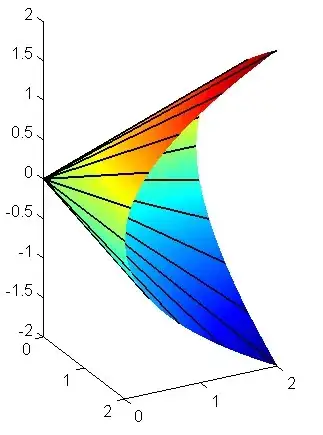
This surface can be rendered in different ways by materializing different curves traced on it. Of course, as it is a cone, it is interesting to materialize it as a ruled surface. It suffices to join point $(0,0,0)$ either to points $(1,t,t^2)$ or to points of the form $(t^2,t,1)$ which both belong to parabolas.

Here is a Matlab program that implements these ideas (please note that the roles of $x$ and $z$ have been exchanged). The generated graphics is below.

clear all;close all;hold on;axis equal;
x = 0:.02:2;

y = 0:.02:2;
set(gcf,'color','w');
[X,Y]=meshgrid (x,y); 
Z=sqrt(X.*Y);
axis([0,2,0,2,-2,2]);
surf(X,Y, Z,'edgecolor','none');shading interp
surf(X,Y,-Z,'edgecolor','none');shading interp
for t=0:0.2:1
plot3([0,2],[0,2*t^2],[0,2*t],'linewidth',1,'color','k');
  plot3([0,2*t^2],[0,2],[0,2*t],'linewidth',1,'color','k');
end;
view([62,24]);

On the following graphics, the vertical axis is for variable $y$.

Edit : In order to broaden the perspective, here are two documents generalizing this issue, both with nice graphics: -1- (this is chapter 5 of the very valuable book of Jon Dattorro entitled "Convex optimization and Euclidean geometry" ; see the end of this chapter) and -2-.

Answer 2

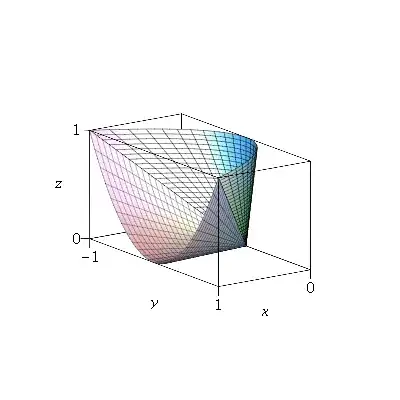
The $2 \times 2$ real symmetric matrix $\pmatrix{x & y\cr y & z\cr}$ is positive semidefinite iff $x \ge 0$, $z \ge 0$ and $xz - y^2 \ge 0$. We will want to represent this by $(x,y,z)$ in $\mathbb R^3$. It looks like you're taking the intersections with $x=1$ and with $z=1$. For $x=1$ the condition is $z \ge y^2$ and for $z=1$ it is $x \ge y^2$. So we plot the curves $(x,y,z) = (1,y,y^2)$, $-1 \le y \le 1$ and $(x,y,z) = (y^2, y, 1)$, $-1 \le y \le 1$. Then we join several points on each of these curves to $(0,0,0)$ by straight lines.

I don't do much plotting in Matlab. In Maple I would do something like this:

plots:-display(plot3d([t,t*y,t*y^2],t=0..1,y=-1..1),
  plot3d([t*y^2,t*y,t],t=0..1,y=-1..1),
  labels=[x,y,z],tickmarks=[2,2,2],scaling=constrained,lightmodel=light1);

Answer 3

syms x y z

f = x*z - y^2; 

fimplicit3(f, [0 1 -1 1 0 1],'EdgeColor','none')

positive semidefinite cone: