Every permutation is a product of two permutations of order 2

Question

I am trying to solve a problem, not for homework, and it has me stomped!

For $n\geq 4$ and $\alpha\in S_n$, $$\alpha=\dot{\alpha}\dot{\beta}$$ where $\dot{\alpha},\dot{\beta}$ are of order 2.

I know that every permutation can be expressed as a product of transpositions.

In my attempt to solve the problem I have focused on cyclic permutations, as every permutation is a product of disjoint cyclic permutations.

Using the fact that, for $4<k\leq n$$$(a_1\ a_k)(a_1\ a_2\ \cdots\ a_{k-1})=(a_1\ a_2\ \cdots\ a_k),$$ I found that if $k$ is even then $$(a_1\ a_2\ \cdots\ a_k)=[(a_1\ a_k)(a_{k-1} a_{k-2})\cdots (a_{k-2i+1}\ a_{k-2i})](a_{k-2i-1}\ \cdots a_{k-3}\ a_{k-1})$$ where $k-2i+1=3$, and if $k$ is odd then $$(a_1\ a_2\ \cdots\ a_k)=[(a_1\ a_k)(a_{k-1} a_{k-2})\cdots (a_{k-2i+1}\ a_{k-2i})](a_{k-2i+1}\ \cdots a_{k-3}\ a_{k-1})$$ where $k-2i+1=2$.

I am wondering, is this the correct route to take in order to resolve this problem? Or, is there another way? Could someone point me in the right direction?

Answer 1

I think you are working in the right direction. Essentially, you build upon the following formulas (note that I compose permutations left-to-right)

$$ (12) \cdot (23) = (132) $$

$$ (12)(34) \cdot (23) = (1342) $$

$$ (12)(34) \cdot (23) (45) = (13542) $$

$$ (12)(34) \dots \cdot (23) (45) \dots = (135 \dots 6 4 2). $$

Answer 2

As an example of decomposing a cycle into two sets of transpositions:

Answer 3

An explicit decomposition of the cycle $(12...n)$ is also given by the product of $r(12)r(34...n)$ and $r(123)r(4...n)$ where $r$ means order reversal, i.e. $r(123)$ maps $123$ to $321$. Clearly each factor is of order 2.

Answer 4

First note that a (finite) permutation has order 2 precisely when it is not the identity and equals a product of disjoint transpositions. We use this repeatedly without mention.

The claim reduces to the case of cyclic permutations as we shall see in a moment. For now consider the generic cyclic permutation $(12\cdots n)$ of order $n\geq 3$. Then we have that $(12\cdots n)= \dot{\alpha}\dot{\beta}$, where

$$\dot{\alpha}= \prod_{j=1}^{\lfloor n/2 \rfloor}(n+1-j,j+1)$$ $$\dot{\beta}= \prod_{j=1}^{\lceil n/2 \rceil}(n+1-j,j)$$

(I added commas to the cycle notation for readability.)

Since the transpositions in the products are disjoint, both $\dot{\alpha}$ and $\dot{\beta}$ have order 2.

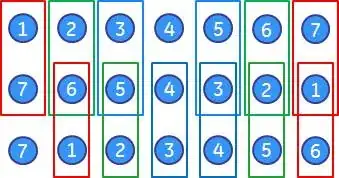
I derived the these formulas by guiding myself with some graphical representations of $\dot{\alpha}$ and $\dot{\beta}$. I include them for $n=3,4,5,6$in case it helps descifring what these permutations do. Blue edges represent transpositions in $\dot{\alpha}$ and green edges represent transpositions in $\dot{\beta}$.

Graphical representation of $\dot{\alpha}$ and $\dot{\beta}$ for $n=3,4,5,6$.

With this tool at our disposal, consider now an arbitrary permutaion $\alpha\in S_n$ for $n\geq 4$. Write $\alpha$ as a product of disjoint cycles $\alpha = c_1c_2\cdots c_k$.

Consider the case $k=1$, i.e. $\alpha$ is a cycle. If $\alpha$ is the identity, $\alpha = (12)(12)$. Also if $\alpha= (ab)$ for $a\neq b$ and $c,d$ are other two distinct elements, $\alpha=(cd)((ab)(cd))$. Now, if the order of $\alpha$ is at least three we may apply our previous argument and be done.

(This was the part where we required $n$ to be at least 4. Note that the claim does not hold for a single transposition in $S_3$.)

Now consider the remaining case $k\geq 2$. W.l.o.g. let $c_1,\ldots, c_l$ be all the transpositions among the $c_i$ for $0\leq l \leq k$. If $l=k$, $\alpha$ is a product of at least 2 disjoint transpositions and we are done. For $l<k$, apply the initial construction to write $c_i = a_i b_i$ for $l<i\leq k$, where both $a_i$ and $b_i$ have order 2 and only exchange elements that are within the cycle $c_i$. Thanks to this property $\{a_i,b_i:l<i\leq k\}$ are mututally disjoint permutations for different values of $i$ and we can rearrange them:

$$\alpha = c_1\cdots c_k = c_1\cdots c_l a_{l+1}b_{l+1}\cdots a_k b_k= (c_1\cdots c_l a_{l+1}\cdots a_{k})(b_{l+1}\cdots b_{k})$$

Set $\dot{\alpha}= c_1\cdots c_l a_{l+1}\cdots a_{k}$ and $\dot{\beta}= b_{l+1}\cdots b_{k}$. These permutations have order two and none of them is the identity since $l<k$. This concludes the proof.