21

Conjecture:

For each $n\in\mathbb N$ there are primes $q<p$ with $p-q=2^n$.

Verified for $n\leq 26$:

 n        p  q
 0        3  2
 1        5  3
 2        7  3
 3       11  3
 4       19  3
 5       37  5
 6       67  3
 7      131  3
 8      263  7  
 9      523 11  
10     1031  7  
11     2053  5  
12     4099  3  
13     8209 17  
14    16421 37  
15    32771  3  
16    65539  3  
17   131101 29  
18   262147  3  
19   524341 53  
20  1048583  7  
21  2097169 17  
22  4194371 67
23  8388619 11  
24 16777259 43  
25 33554473 41  
26 67108961 97

Proofs or counterexamples may be far away, but is something known about this topic?

Caleb Stanford
  • 47,093
Lehs
  • 14,252
  • 4
  • 28
  • 82
  • 3
    This follows from Shinzel's Hypothesis H. Indeed that hypothesis would show that every even number can be written as the difference of two primes. Of course, little is known by way of actual proofs of specific cases. – lulu Jul 16 '16 at 16:16
  • 3
    According to this Chen's work on the Goldbach conjecture also implies that every (sufficiently large?) even number is the difference between a prime and a $P_2$ (a product of two primes). – lulu Jul 16 '16 at 16:21
  • 2
    This is a special case of an open problem,that every even number can be written as a difference of two primes.I believe it is true,but it seems to be an extremely difficult problem. – Konstantinos Gaitanas Jul 16 '16 at 18:00
  • 3
    Some more terms at OEIS A056206. – Raymond Manzoni Jul 16 '16 at 23:13
  • 2
    This is a great question. – Caleb Stanford Jul 18 '16 at 18:59
  • @EnjoysMath: Do you suggest there are patterns or that I should present the examples better? – Lehs Aug 14 '18 at 18:18
  • 1
    Green and Tao say that there are infinitely many arithmetic progressions of arbitrary length $k$ of prime numbers. If we take some prime $p$ and look at a progression of period $2^m$, then there should be a progression of length $2^n$ such that $p+2^{m+n}=q$, $q$ being prime. Not quite a proof because Green and Tao don't say that arbitrarily long progression can have any chosen period. But since primes have the form $4j \pm 1$, a period of $2^n$ is not an unreasonable expectation. But not, as I said, a proof. – Keith Backman Aug 15 '18 at 02:09

1 Answers1

1

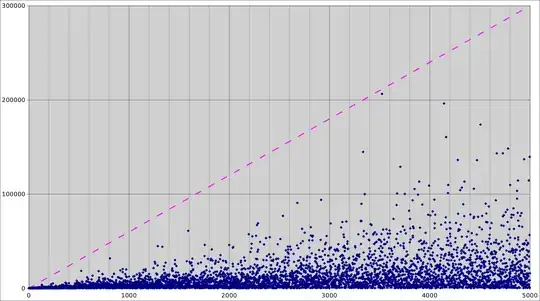Smallest q such that <span class=$2^n+q$ is prime" />

Not an answer but AFAIK one can not add an image to a comment:

I continued the data from https://oeis.org/A056206 up to n=5000 and made a scatter plot.

The magenta dashed line is $60n \ll 2^n$.

Again this is no proof but its seems it is safe to assume there is always a prime $q<n^2$.

The average prime gap for p is about $nlog(2)$.

There are on average at least n primes between p and $p+n^2$ giving us $\frac{n}{log(n)}$ solutions also being prime (q).

pietfermat
  • 602