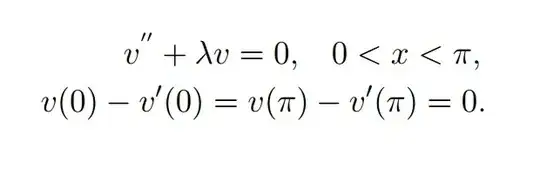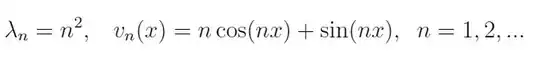Integration By Parts stuck

Question

Given this S-L problem with solution:

And I want to prove this equality when $f(x)$ also has the same conditions as S-L problem.

I tried doing integration by parts on the left side twice but didn't end anywhere.. But I know it's the way to solve it.. any help?

But what did you get after integrating by parts? – Yuriy S Jul 16 '16 at 15:50 — Yuriy S, Jul 16 '16 at 15:50

score 1 · Accepted Answer · answered Jul 16 '16 at 16:10

1

Integration by parts yields: $$\int_0^\pi f''(x)v_n(x)dx=$$ $$v_n(\pi)f'(\pi)-v'_n(\pi)f(\pi)-v_n(0)f'(0)+v'_n(0)f(0)-\lambda_n\int_0^\pi f(x)v_n(x)dx $$

(Kindly see my answer here for a quick way to integrate by parts).

Since $f(x)$ has the same conditions as $v(x)$, then the first four terms cancel out, leaving you with the desired result.

answered Jul 16 '16 at 16:10

entrelac

4,781

Just one question, This what I'm getting: $v_n(\pi)f'(\pi)-v'_n(\pi)f(\pi)-v_n(0)f'(0)+v'_n(0)f(0)+\int_0^\pi f(x)v_n(x)dx$ How are you getting this $\lambda$ ? – Sijaan Hallak Jul 16 '16 at 16:34
1

The differential equation. You should get $v_n''(x)$ in that last integral, that you then replace by $-\lambda v_n$ – entrelac Jul 16 '16 at 16:39
Thank you, I got this the whole time though -,- :( – Sijaan Hallak Jul 16 '16 at 16:41

Integration By Parts stuck

1 Answers1